决策树:从根节点开始一步步到叶子节点,所有的数据最后都落到叶子节点里面,既可以用来做分类也可以用来做回归
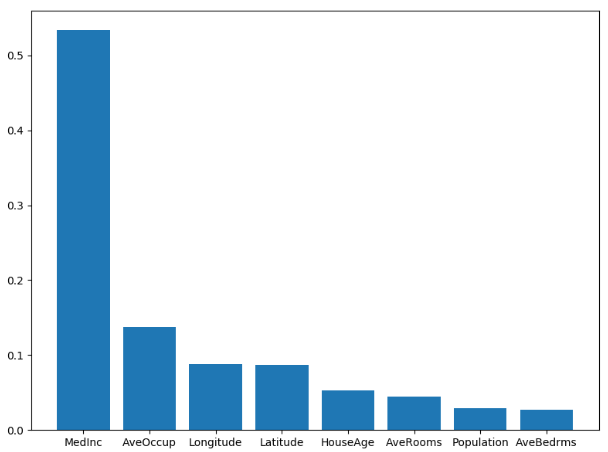
树的组成: 1.根节点(第一个参数)
2.非子叶节点与分支: 中间过程
3. 子叶节点,最终的决策结果
对于一些连续的变量来说,通常使用一刀切的方式。
决策树的训练与测试
训练阶段通过构造一棵树,即选择特征作为这一层的判断
测试:根据构造出来的树结构,将测试数据从上到下走一遍
决策树特征选择的衡量标准
对每一个特征把数据分开后,求一个熵值,熵值越大,表示当前叶子节点的混乱度越高
熵值的公式: -∑p*logp p表示的是概率
不确定性越高,熵值越大,物体概率为0和1时,熵值最小,当物体的概率为0.5时,熵值越大
在ID3中,使用信息增益,即没经过特征删选前的熵和经过特征删选后的熵之差,即不确定性的降低(两熵之差)
对于熵求解和信息增益的实例
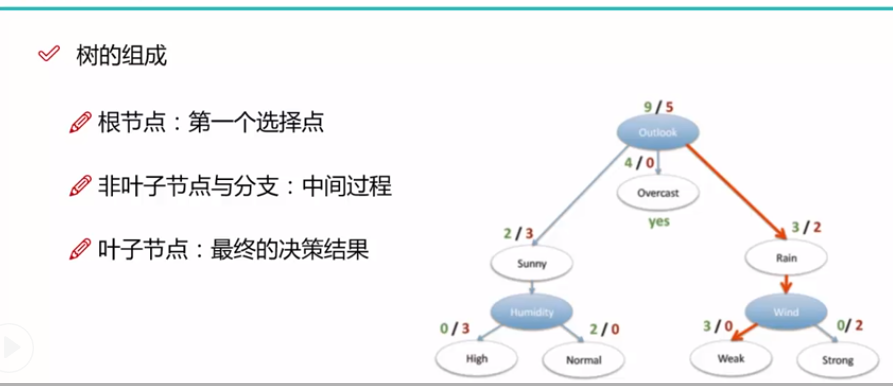
下面使用了4个特征,判断的结果是是否去打球
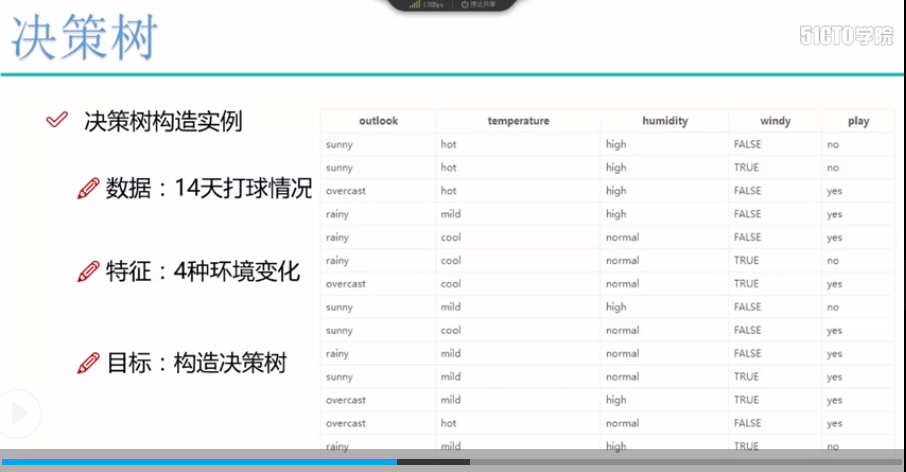

上述以天气特征做一个说明:
没有根据特征进行区分的时候,所有样本都在一个叶子节点中,根据计算公式:熵 = -9/14*log9/14 - 5/14*log5/14 = 0.940
使用天气进行特征分离时,有sunny, overcast, rainy,根据特征的类别分成3个叶子节点
第一个叶子节点的标签为 2个yes, 3个no 熵 = -2/5*log(2/5) - 3/5*log(3/5) = 0.971
第二个叶子节点的标签为4个yes 熵 = -5/5 * log(5/5) = 0
第三个叶子节点的标签为3个yes, 2个no 熵 = -3/5*log3/5 - 2/5*log2/5 = 0.971
总的熵为: 5/14 * 0.971 + 4/14*0 + 5/14 * 0.971 = 0.693
信息增益 = 0.940 - 0.639 = 0.247
通过相同的方法,求得其他特征所获得的信息增益,来判断哪一个特征作为叶子节点的判别特征
信息增益率: C4.5
对于像ID这样的特征,可以把每一个样本都进行分开,因为单独的样本,信息熵是等于0,但是明显的ID特征不具有判别性,因此引入了信息增益率
即 在原来的基础上除于叶子节点的个数, 即 假如id有3个, 那么此时的熵 = (-1/3log1/3) * 1/3 * 3 , 此时的熵值还是很大的,这样id特征就会被弃用
CART: 使用gini系数来作为衡量标准, GINI = 1 - ∑p^2 p表示概率,概率越小,熵值越大
对于连续的特征,我们该如何选择分界点,这里我们使用贪心算法,将每种可能性都试一遍,首先将特征进行排序,比如身高特征:60, 75, 80, 85, 90, 95, 100, 120, 125, 220, 如果进行二分,这里有9个分界点,选择一个能将数据尽量分开的分界点,即熵值最小的分界点
决策树的剪枝策略,、
目的: 为了防止由于决策树过大,而导致的过拟合的风险
剪枝策略: 预剪枝 , 后剪枝
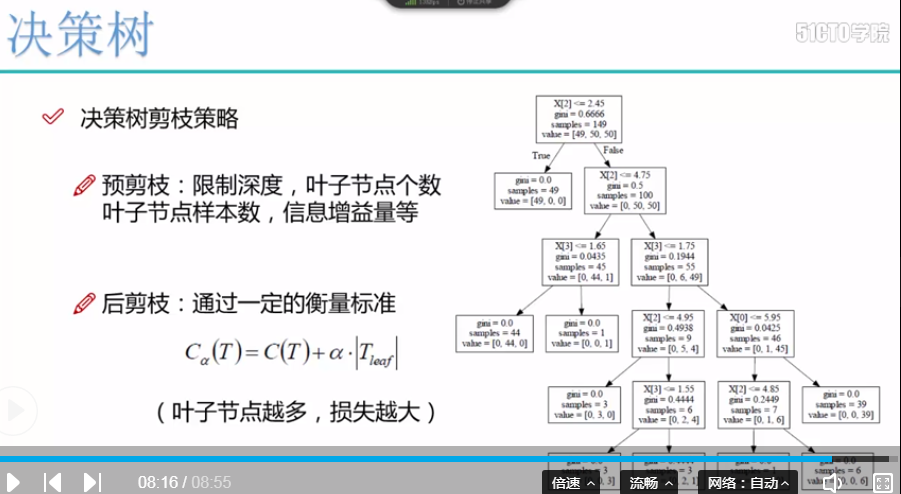
预剪枝:边建立决策树边进行剪枝操作(更实用) 控制树的深度, 叶子节点的个数,叶子节点的样本数,信息增益量
后剪枝: 通过一定的衡量标准
损失函数:Ca(T) = C(T) + a(Teaf) C(T)表示gini系数*样本数, a表示惩罚因子, Teaf表示叶子节点的个数,叶子节点越多,惩罚的越多,损失函数越大
sklearn决策树中所涉及的参数
1.criterion gini or entropy 使用gini系数还是使用熵
2.splitter best or random 前者是所有特征找到最好的切分点,后者是随机特征,这样在特征多的时候,降低运行速度
3.max_features None(所有) 当样本的特征量小于50时,使用所有的
4.max_depth 表示最大的树深度
5.min_samples_split 叶子节点最小的样本数,当小于这个值时就不进行分割
6.min_samples_leaf 如果某叶子节点的个数小于样本数,那么该叶子节点和兄弟节点将被一起剪枝
7.min_weight_fraction_leaf 叶子节点所有样本权重和的最小值,如果样本的分布类型偏差很大就会引入这个值
8.max_leaf_nodes 限制最大叶子节点数
9.class_weight 指定样本各类别的权重,主要防止训练集某些类型的样本过多导致训练的决策树过于偏向这些类别
10.min_impurity_split 这个值限制了决策树的增长,比如信息增益,基尼系数小于阈值就停止增长
代码:
1.选择max_depth进行树的可视化展示
2.进行决策树代码的实例化
3.使用GridSeach网格搜索进行参数的选择
4. 根据rfr.feature_importances_ 得分特征的重要性比例
# 1 决策树的可视化展示 from sklearn import tree from sklearn.datasets.california_housing import fetch_california_housing housing = fetch_california_housing() dtr = tree.DecisionTreeRegressor(max_depth=2) dtr.fit(housing[:, [6, 7]], housing.target) dot_data = tree.export_graphviz( dtr, out_file = None, feature_names=housing.feature_name[6:8], filled = True, impurity = False, rounded = True ) import pydotplus graph = pydotplus.graph_from_dot_data(dot_data) graph.get_nodes()[7].set_fillcolor('#FFF2DD') from IPython.display import Image Image(graph.create_png()) # 2.决策树使用实例 # from sklearn import tree from sklearn.cross_validation import train_test_split # # # 数据拆分 train_x, test_x, train_y, test_y = train_test_split(housing.data, housing.target, test_size=0.1, random_state=42) # 建立决策树 dtr = tree.DecisionTreeRegressor(random_state=42) # 训练数据 dtr.fit(train_x, train_y) # 打印出dtr得分, 这里的得分表示的是准确率 print(dtr.score(test_x, test_y)) # 3. 使用GridSearch进行组合参数选择 from sklearn.grid_search import GridSearchCV from sklearn.ensemble import RandomForestRegressor from sklearn.datasets.california_housing import fetch_california_housing # 载入数据 housing = fetch_california_housing() # 列出参数列表 tree_grid_parameter = {'min_samples_split':list((3, 6, 9)), 'n_estimators':list((10, 50, 100))} # 进行参数的搜索组合 grid = GridSearchCV(RandomForestRegressor(), param_grid=tree_grid_parameter, cv=3) grid.fit(train_x, train_y) print(grid.grid_scores_) # 打印得分 print(grid.best_params_) # 打印最好的参数组合 print(grid.best_score_) # 打印最好的得分 # 4. 显示出随机森林特征的重要性,并做条形图 import pandas as pd import matplotlib.pyplot as plt rfr = RandomForestRegressor(min_samples_split=6, n_estimators=100) rfr.fit(train_x, train_y) print(rfr.score(test_x, test_y)) # 使用pd.Series进行组合,值是特征重要性的值,index是样本特征 feature_important = pd.Series(rfr.feature_importances_, index = housing.feature_names).sort_values(ascending=False) figure = plt.figure(figsize=(8, 6)) plt.bar(feature_important.index, feature_important.data) plt.show()
特征重要性图