http://acm.hdu.edu.cn/showproblem.php?pid=1890
Robotic Sort
Problem Description
Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes.
In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.
Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.
A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.
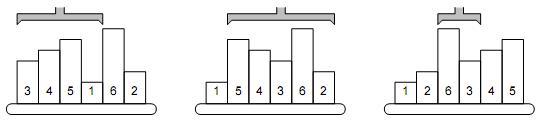
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.
Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.
In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.
Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.
A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.

The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.
Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.
Input
The input consists of several scenarios. Each scenario
is described by two lines. The first line contains one integer number N , the
number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N
space-separated positive integers, they specify the heights of individual
samples and their initial order.
The last scenario is followed by a line containing zero.
The last scenario is followed by a line containing zero.
Output
For each scenario, output one line with exactly N
integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.
Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.
Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.
Sample Input
6
3 4 5 1 6 2
4
3 3 2 1
0
Sample Output
4 6 4 5 6 6
4 2 4 4
题意:给出一个长度为n的无序数列a,然后按照一定规则进行反转,到第i个点时,找一个区间[a,b],a=i,b是第i大元素所在的下标,然后把区间进行反转,如果存在多个相同大小的元素,则要保证他们在原始数列的相对顺序不变
分析:对于原始数列,把他们每个数对应的key值依次初始化为1-n,然后用p[i].val记录第i个点值,p[i].pri记录第i个值是第几次出现,主要解决相对位置问题,p[i].key记录第i个元素对应的key值,然后把p从小到大排序,当搜索到第i个元素的时候,则p[i].val就是第i大元素,根据p[i].key在splsy树中找出该键值在序列中的实际顺序下标b,然后把第a-1个元素反转到树根,把第b+1个旋转到树根的右儿子出,然后对树根的右儿子的左儿子进行标记
code:

#include"stdio.h" #include"iostream" #include"queue" #include"string.h" #include"map" #include"stdlib.h" #include"algorithm" #include"string" #define M 1000005 #define inf 0x3f3f3f3f using namespace std; int a[M]; struct P { int val,pri,key; }p[M]; int top,root; int cmp(P a,P b) { if(a.val==b.val) return a.pri<b.pri; return a.val<b.val; } int son[M][2],fa[M],num[M],flip[M],child[M]; struct Text { queue<int>q; void init(int n) { top=n+2; for(int i=0;i<=n+2;i++) { num[i]=1; son[i][0]=son[i][1]=-1; fa[i]=-1; flip[i]=0; } } void Rotate(int x,int k) { int y=fa[x]; son[y][1^k]=son[x][k]; if(son[y][1^k]!=-1) fa[son[y][1^k]]=y; push_up(y); if(son[fa[y]][0]==y) son[fa[y]][0]=x; else son[fa[y]][1]=x; fa[x]=fa[y]; son[x][k]=y; fa[y]=x; } void splay(int x,int f) { if(x==-1)return; while(fa[x]!=f) { int y=fa[x]; int z=fa[y]; if(z==f) { if(son[y][0]==x) Rotate(x,1); else Rotate(x,0); } else { if(son[z][0]==y) { if(son[y][0]==x) { Rotate(y,1); Rotate(x,1); } else { Rotate(x,0); Rotate(x,1); } } else { if(son[y][1]==x) { Rotate(y,0); Rotate(x,0); } else { Rotate(x,1); Rotate(x,0); } } } } if(f==top) root=x; } void RotateTo(int k,int f) { k++; int x=root; while(1) { push_down(x); int temp=getNum(son[x][0])+1; if(k==temp)break; else if(k<temp) x=son[x][0]; else { k-=temp; x=son[x][1]; } } splay(x,f); push_up(x); } int getOrder(int x) { int y=x; while(fa[y]!=top) { int f=fa[y]; child[f]=y; y=fa[y]; } y=root; while(y!=x) { int z=child[y]; push_down(z); y=child[y]; } int k=getNum(son[x][0])+1; while(fa[x]!=top) { int y=fa[x]; int temp=getNum(son[y][0])+1; if(son[y][0]==x) x=fa[x]; else { k+=temp; x=fa[x]; } } return k-1; } void Reversal(int x) { if(x==-1)return; int y=son[x][0]; son[x][0]=son[x][1]; son[x][1]=y; } int getNum(int x) { if(x==-1)return 0; return num[x]; } void push_up(int x) { num[x]=getNum(son[x][0])+getNum(son[x][1])+1; } void push_down(int x) { if(x==-1)return; if(flip[x]) { flip[x]^=1; Reversal(x); if(son[x][0]!=-1) flip[son[x][0]]^=1; if(son[x][1]!=-1) flip[son[x][1]]^=1; } } void creat(int l,int r,int k,int f) { if(l>r)return; int mid=(l+r)/2; if(f==top) root=mid; son[f][k]=mid; fa[mid]=f; creat(l,mid-1,0,mid); creat(mid+1,r,1,mid); push_up(mid); } void dfs(int x,int n) { if(x==-1)return; push_down(x); dfs(son[x][0],n); if(x>=1&&x<=n) q.push(a[x]); dfs(son[x][1],n); } void output(int n) { dfs(root,n); printf("%d",q.front()); q.pop(); while(!q.empty()) { printf(" %d",q.front()); q.pop(); } puts(""); } }; int main() { int n; while(scanf("%d",&n),n) { Text text; for(int i=1;i<=n;i++) scanf("%d",&a[i]); map<int,int>mp; p[0].val=-inf; p[0].pri=0; p[0].key=0; for(int i=1;i<=n;i++) { p[i].val=a[i]; p[i].pri=mp[a[i]]; p[i].key=i; mp[a[i]]++; } p[n+1].val=inf; p[n+1].pri=0; p[n+1].key=n+1; sort(p,p+n+2,cmp); text.init(n); text.creat(0,n+1,0,top); for(int i=1;i<=n;i++) { int l=i-1; int key=p[i].key; int r=text.getOrder(key)+1; text.RotateTo(l,top); text.RotateTo(r,root); flip[son[son[root][1]][0]]^=1; //text.output(n); if(i==1) printf("%d",r-1); else printf(" %d",r-1); } puts(""); } return 0; }
