题意:给定质数p,求q!模p的值,其中q为小于p的最大质数
1e9<=p<=1e14
思路:根据质数密度近似分布可以暴力找q并检查
找到q后根据威尔逊定理: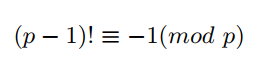
把q+1到p-1这一段的逆元移过去
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 typedef unsigned int uint; 5 typedef unsigned long long ull; 6 typedef pair<int,int> PII; 7 typedef pair<ll,ll> Pll; 8 typedef vector<int> VI; 9 #define N 110000 10 #define M 1100000 11 #define fi first 12 #define se second 13 #define MP make_pair 14 #define pi acos(-1) 15 #define mem(a,b) memset(a,b,sizeof(a)) 16 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++) 17 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--) 18 #define lowbit(x) x&(-x) 19 #define Rand (rand()*(1<<16)+rand()) 20 #define id(x) ((x)<=B?(x):m-n/(x)+1) 21 #define ls p<<1 22 #define rs p<<1|1 23 24 const ll MOD=998244353,inv2=(MOD+1)/2; 25 double eps=1e-6; 26 ll INF=1e14; 27 28 29 int read() 30 { 31 int v=0,f=1; 32 char c=getchar(); 33 while(c<48||57<c) {if(c=='-') f=-1; c=getchar();} 34 while(48<=c&&c<=57) v=(v<<3)+v+v+c-48,c=getchar(); 35 return v*f; 36 } 37 38 int prime(ll x) 39 { 40 ll t=sqrt(x); 41 for(ll i=2;i<=t;i++) 42 if(x%i==0) return 0; 43 return 1; 44 } 45 46 ll mult(ll a,ll b,ll p) 47 { 48 ll t=(a*b-ll((long double)a/p*b+1e-3)*p)%p; 49 return t<0?t+p:t; 50 } 51 52 ll pw(ll x,ll y,ll p) 53 { 54 ll t=1; 55 while(y) 56 { 57 if(y&1) t=mult(t,x,p); 58 x=mult(x,x,p); 59 y>>=1; 60 } 61 return t; 62 } 63 64 int main() 65 { 66 //freopen("1.in","r",stdin); 67 //freopen("1.out","w",stdout); 68 int cas=read(); 69 while(cas--) 70 { 71 ll n; 72 scanf("%I64d",&n); 73 ll k=n-2; 74 if(n==3) k=2; 75 else 76 { 77 while(k&&!prime(k)) k-=2; 78 } 79 ll ans=n-1; 80 //printf("k=%I64d ",k); 81 for(ll i=k+1;i<=n-1;i++) 82 { 83 //printf("i=%I64d ",i); 84 ll t=pw(i,n-2,n); 85 //printf("inv%I64d=%I64d ",i,t); 86 ans=mult(ans,t,n); 87 } 88 89 90 printf("%I64d ",ans); 91 } 92 return 0; 93 }