题意:

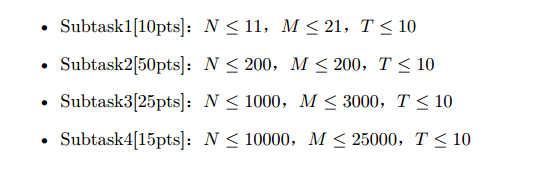
思路:这道题并没有官方题解
没有羊驼在所有三元组中出现就是NO
现在考虑不少于1只的情况
删去其中一只,我们得到了两组点和一些边
我们只要判断这是否为一张二分图,使用暴力染色的方法就有60分了
1 #include<cstdio> 2 #include<algorithm> 3 #define N 10010 4 #define M 50010 5 using namespace std; 6 int T,n,m,edgenum,u,v,ok,isok,root; 7 int f[N],vet[M],next[M],head[N],a[M],b[M],c[M],vis[N],flag[N],col[N]; 8 void add(int u,int v) 9 { 10 vet[++edgenum]=v; 11 next[edgenum]=head[u]; 12 head[u]=edgenum; 13 } 14 void dfs(int u) 15 { 16 vis[u]=1; 17 for (int e=head[u];e;e=next[e]) 18 { 19 int v=vet[e]; 20 if (flag[v]) continue; 21 if (vis[v]) 22 { 23 if (col[v]==col[u]) ok=0; 24 }else 25 { 26 col[v]=col[u]^1; 27 dfs(v); 28 } 29 } 30 } 31 int main() 32 { 33 freopen("river.in","r",stdin); 34 freopen("river.out","w",stdout); 35 scanf("%d",&T); 36 while (T--) 37 { 38 scanf("%d%d",&n,&m); 39 for (int i=1;i<=n;i++) f[i]=0; 40 for (int i=1;i<=m;i++) 41 { 42 scanf("%d%d%d",&a[i],&b[i],&c[i]); 43 f[a[i]]++;f[b[i]]++;f[c[i]]++; 44 } 45 root=-1; 46 for (int i=1;i<=n;i++) if (f[i]==m) root=i; 47 if (root==-1){puts("no");continue;} 48 edgenum=0; 49 for (int i=1;i<=n;i++) head[i]=0; 50 for (int i=1;i<=m;i++) 51 { 52 if (a[i]==root){u=b[i];v=c[i];} 53 if (b[i]==root){u=a[i];v=c[i];} 54 if (c[i]==root){u=a[i];v=b[i];} 55 //ed[i].x=u;ed[i].y=v; 56 add(u,v);add(v,u); 57 } 58 isok=0; 59 //printf("%d ",root); 60 for (int i=1;i<=n;i++) if (i!=root) 61 { 62 if (isok) break; 63 for (int j=i+1;j<=n;j++) if (j!=root) 64 { 65 //printf("%d %d ",i,j); 66 for (int k=1;k<=n;k++) vis[k]=col[k]=0; 67 flag[i]=flag[j]=1; 68 ok=1; 69 for (int k=1;k<=n;k++) if (!vis[k]&&k!=i&&k!=j&&k!=root) 70 dfs(k); 71 if (ok) isok=1; 72 flag[i]=flag[j]=0; 73 if (isok) break; 74 } 75 } 76 if (isok) puts("yes");else puts("no"); 77 } 78 }
至于标程……谁看得懂呢……貌似是暴力加了点优化……
1 #include<bits/stdc++.h> 2 #define FT first 3 #define SC second 4 #define PB push_back 5 #define MP make_pair 6 #define REP(i, l, r) for(int i = (l); i <= (r); i++) 7 #define PER(i, r, l) for(int i = (r); i >= (l); i--) 8 #define FOR(i, n) for(int i = 0; i < (n); i++) 9 #define ROF(i, n) for(int i = (n) - 1; i >= 0; i--) 10 #define VEP(i, x) for(int i = 0; i < x.size(); i++) 11 #define DFOR(i, x, y) for(int i = hd[x], y = e[i].to; i; i = e[i].nxt, y = e[i].to) 12 #define MEM(a, b) memset(a, b, sizeof(a)) 13 #define rint read<int>() 14 #define rll read<LL>() 15 16 using namespace std; 17 typedef long long LL; 18 typedef long double LD; 19 typedef pair<int, int> PI; 20 const int inf = 0x7fffffff; 21 const int MOD = 1000000007; 22 23 template <typename tn> 24 inline tn read(){ 25 char ch; tn f = 1; 26 while (!isdigit(ch = getchar())) if (ch == '-') f = -1; 27 tn x = ch - '0'; 28 while (isdigit(ch = getchar())) x = x * 10 + ch - '0'; 29 return x * f; 30 } 31 template <typename tn> inline void cmax(tn &a, tn b){ if (a < b) a = b; } 32 template <typename tn> inline void cmin(tn &a, tn b){ if (a > b) a = b; } 33 34 const int N = 10000 + 5; 35 struct Edge{ int nxt, to; } e[N * 6]; 36 struct Data{ int f, safe, danger; }; 37 int color[N], x[N], y[N], z[N], sz[N], rt, tail, hd[N], tot, dep[N], S, T; 38 void add(int x, int y){ e[++tail] = (Edge){hd[x], y}, hd[x] = tail; } 39 Data dfs(int x, int c, int f){ 40 color[x] = c; 41 Data cur; 42 cur.safe = inf, cur.danger = -1, cur.f = 0; 43 DFOR(i, x, y) if (y != f && color[y] != -2) 44 if (!~color[y]){ 45 dep[y] = dep[x] + 1; 46 Data now = dfs(y, c ^ 1, x); 47 cur.f += now.f; if (cur.f > 1) { return cur;} 48 cmin(cur.safe, now.safe), cmax(cur.danger, now.danger); 49 } else if (dep[y] < dep[x]) if (color[x] ^ color[y]) cmin(cur.safe, dep[y]); else{ 50 cmax(cur.danger, dep[y]); 51 if (!S) S = x, T = y; 52 if (S != x && S != y) S = -1; 53 if (T != x && T != y) T = -1; 54 } 55 if (cur.safe <= dep[x] && cur.danger >= dep[x]) cur.f = 100; 56 else if (cur.danger >= dep[x]) cur.f++, cur.danger = -1; 57 return cur; 58 } 59 int main(){ 60 freopen("river.in", "r", stdin); 61 freopen("river.out", "w", stdout); 62 int Cas = rint; 63 while (Cas--){ 64 int n = rint, m = rint; 65 MEM(sz, 0), MEM(hd, 0), tail = 0, rt = 0; 66 REP(i, 1, m) sz[x[i] = rint]++, sz[y[i] = rint]++, sz[z[i] = rint]++; 67 REP(i, 1, n) if (sz[i] == m) rt = i; 68 if (rt){ 69 bool ans = 0; 70 REP(i, 1, m){ 71 if (x[i] == rt) swap(x[i], z[i]); 72 if (y[i] == rt) swap(y[i], z[i]); 73 add(x[i], y[i]), add(y[i], x[i]); 74 } 75 REP(i, 1, n) if (i != rt) { 76 MEM(color, -1), color[i] = -2; 77 int flag = 1, tot = 0; 78 REP(i, 1, n) if (color[i] == -1){ 79 S = 0, T = 0; 80 int tmp = dfs(i, 0, 0).f; 81 if (S > 0 || T > 0) cmin(tmp, 1); 82 tot += tmp; 83 if (tot > 1) {flag = 0; break;} 84 } 85 if (flag) {ans = 1; break;} 86 } 87 if (ans) printf("yes "); else printf("no "); 88 } else printf("no "); 89 } 90 }