关于图的几个概念定义:
- 连通图:在无向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该无向图为连通图。
- 强连通图:在有向图中,若任意两个顶点vivi与vjvj都有路径相通,则称该有向图为强连通图。
- 连通网:在连通图中,若图的边具有一定的意义,每一条边都对应着一个数,称为权;权代表着连接连个顶点的代价,称这种连通图叫做连通网。
- 生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
- 最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。

两个最小生成树(Minimum Spanning Tree, MST)算法完全等价。
如果输入邻接矩阵,一般用Prim。
如果输入边表,一般用Kruskal。
1.Kruskal算法
时间复杂度和把所有边排序的复杂度一样,为O(m log m)O(mlogm)。
如果只需要求最小生成树的最大边的权值,可以在O(m)O(m)的时间内求出。
(二分,每次丢掉一半)
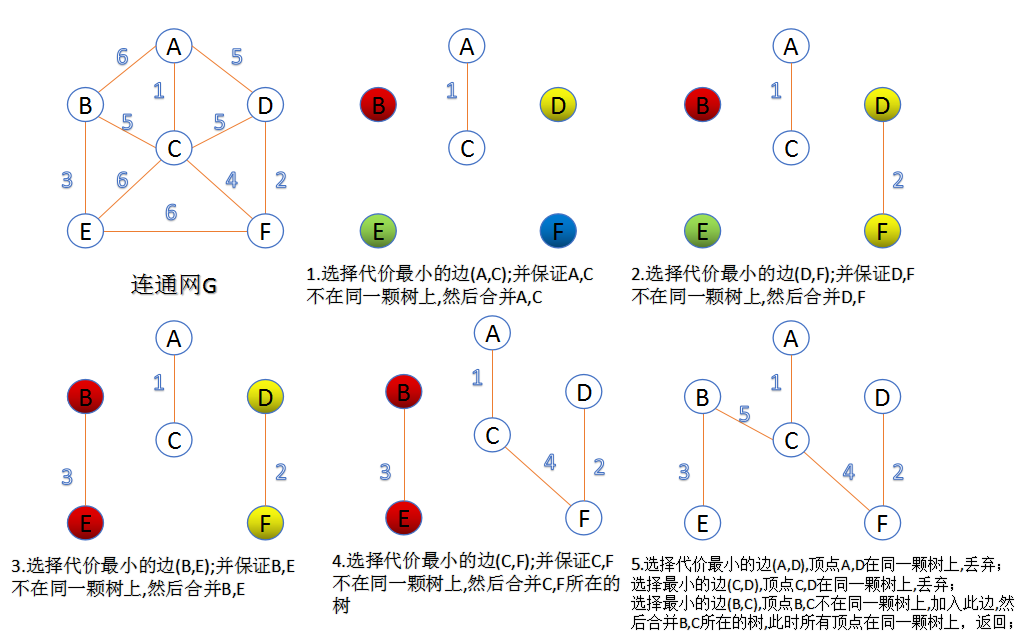
此算法可以称为“加边法”,初始最小生成树边数为0,每迭代一次就选择一条满足条件的最小代价边,加入到最小生成树的边集合里。
1. 把图中的所有边按代价从小到大排序;
2. 把图中的n个顶点看成独立的n棵树组成的森林;
3. 按权值从小到大选择边,所选的边连接的两个顶点ui,viui,vi,应属于两颗不同的树,则成为最小生成树的一条边,并将这两颗树合并作为一颗树。
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。
代码:
1 struct node 2 { 3 //x,y表示边的左右端点,value表示边的值 4 int x,y,value; 5 }no[205]; 6 //n表示点数,m表示边数 7 int n,m; 8 //fa表示树上的顶点 9 int fa[105]; 10 //初始化 11 void init() 12 { 13 //开始时顶点是自己 14 for(int i=0;i<=n;i++) 15 { 16 fa[i]=i; 17 } 18 } 19 //查找顶点 20 int find(int x) 21 { 22 //如果找到顶点,则返回 23 if(fa[x]==x) 24 { 25 return x; 26 } 27 //递归查找x的上一个点的上一个点,同时压缩路径 28 return fa[x]=find(fa[x]); 29 } 30 //排序,按边的值从小到大 31 bool cmp(node a,node b) 32 { 33 return a.value<b.value; 34 } 35 //最小生成树Kruskal算法 36 int kruskal() 37 { 38 //对边进行排序 39 sort(no+1,no+m+1,cmp); 40 //初始化数据 41 init(); 42 //ans表示最小生成树的权值和,cnt表示已经连接的边数 43 int ans=0,cnt=0; 44 //遍历所有边 45 for(int i=1;i<=m;i++) 46 { 47 //如果连接了n-1个边,则表示已经连接所有的点了 48 if(cnt==n-1) 49 { 50 break; 51 } 52 //记录当前边的两边端点的顶点 53 int fx=find(no[i].x),fy=find(no[i].y); 54 //如果他们不相等则进行操作 55 if(fx!=fy) 56 { 57 //将fx的顶点变成fy,相当于把fx这个树的顶点挂在fy这个树顶的下面 58 fa[fx]=fy; 59 //生成树的边数加1 60 cnt++; 61 //加上这个边的权值 62 ans+=no[i].value; 63 } 64 } 65 //如果连了n-1条边则表示有最小生成树 66 if(cnt==n-1) 67 { 68 return ans; 69 } 70 else 71 { 72 return -1; 73 } 74 }
2.Prim算法
可以使用堆优化,类似Dijkstra,但是使用堆优化,效率未必提高。
对于完全图的情况:
不使用堆优化,时间复杂度为O(n^2)O(n2);
使用堆优化,时间复杂度为O(n^2 log n)O(n2logn)。
所以说对于以邻接矩阵输入的图,没必要去用Kruskal。
设图G顶点集合为U,首先任意选择图G中的一点作为起始点a,将该点加入集合V,再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小,此时将b点也加入集合V;以此类推,现在的集合V={a,b},再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小,此时将c点加入集合V,直至所有顶点全部被加入V,此时就构建出了一颗MST。因为有N个顶点,所以该MST就有N-1条边,每一次向集合V中加入一个点,就意味着找到一条MST的边。
初始状态:
设置2个数据结构:
lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了MST
mst[i]:表示对应lowcost[i]的起点,即说明边<mst[i],i>是MST的一条边,当mst[i]=0表示起点i加入MST
我们假设V1是起始点,进行初始化(*代表无限大,即无通路):
lowcost[2]=6,lowcost[3]=1,lowcost[4]=5,lowcost[5]=*,lowcost[6]=*
mst[2]=1,mst[3]=1,mst[4]=1,mst[5]=1,mst[6]=1,(所有点默认起点是V1)
明显看出,以V3为终点的边的权值最小=1,所以边<mst[3],3>=1加入MST
此时,因为点V3的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=5,lowcost[5]=6,lowcost[6]=4
mst[2]=3,mst[3]=0,mst[4]=1,mst[5]=3,mst[6]=3
明显看出,以V6为终点的边的权值最小=4,所以边<mst[6],6>=4加入MST
此时,因为点V6的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=2,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=6,mst[5]=3,mst[6]=0
明显看出,以V4为终点的边的权值最小=2,所以边<mst[4],4>=4加入MST
此时,因为点V4的加入,需要更新lowcost数组和mst数组:
lowcost[2]=5,lowcost[3]=0,lowcost[4]=0,lowcost[5]=6,lowcost[6]=0
mst[2]=3,mst[3]=0,mst[4]=0,mst[5]=3,mst[6]=0
明显看出,以V2为终点的边的权值最小=5,所以边<mst[2],2>=5加入MST
此时,因为点V2的加入,需要更新lowcost数组和mst数组:
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=3,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=2,mst[6]=0
很明显,以V5为终点的边的权值最小=3,所以边<mst[5],5>=3加入MST
lowcost[2]=0,lowcost[3]=0,lowcost[4]=0,lowcost[5]=0,lowcost[6]=0
mst[2]=0,mst[3]=0,mst[4]=0,mst[5]=0,mst[6]=0
至此,MST构建成功,如图所示:
代码:
1 //存放地图 2 int ma[100][100]; 3 //lowcost存放到起点的距离 4 //mst表示i指向的点, 5 int lowcost[100],mst[100]; 6 //n表示点数 7 int n; 8 //初始化地图 9 void init() 10 { 11 for(int i=0;i<=n;i++) 12 { 13 for(int j=0;j<=n;j++) 14 { 15 //本地到本地的权值为0,到其他点的权值为无穷 16 if(i==j) 17 { 18 ma[i][j]=0; 19 } 20 else 21 { 22 ma[i][j]=INF; 23 } 24 } 25 } 26 } 27 //u表示起点 28 int prim(int u) 29 { 30 //ans表示树上所有边的权值和 31 int ans=0; 32 //初始化lowcost,mst 33 for(int i=1;i<=n;i++) 34 { 35 //将所有指向起点的边录入lowcost中 36 lowcost[i] = ma[u][i]; 37 //所有的点都指向起点 38 mst[i]=u; 39 } 40 //起点已在树上,所以为-1 41 mst[u] = -1; 42 //遍历其他n-1个点 43 for(int i=1;i<n;i++) 44 { 45 //当前最小权值为INF 46 int mi=INF; 47 //当前最小值指向的点是-1 48 int v=-1; 49 //遍历所有的点 50 for(int j=1;j<=n;j++) 51 { 52 //如果该点不在树上,且该点到起点的距离小于当前最小权值 53 if(mst[j]!=-1&&lowcost[j]<mi) 54 { 55 //记录这个较小的点和权值 56 v=j; 57 mi=lowcost[j]; 58 } 59 } 60 //v!=-1表示在所有与树连接的最小权值 61 if(v!=-1) 62 { 63 //将这个点标记 64 mst[v]=-1; 65 //累计这个边的权值 66 ans+=lowcost[v]; 67 //遍所有的点 68 for(int j=1;j<=n;j++) 69 { 70 //如果j不在树上且j到树上的距离比j到v的距离大 71 //更新这个数据,并将mst[j]指向v 72 if(mst[j]!=-1&&lowcost[j]>ma[v][j]) 73 { 74 lowcost[j]=ma[v][j]; 75 mst[j]=v; 76 } 77 } 78 } 79 } 80 //返回树上所有边的权值和 81 return ans; 82 }





