P1622 释放囚犯

${color{Cyan}{>>Question}}$

随着题量的上升,见的模型也越来越多

动态规划,明确的状态定义,明确的转移,明确的边界(有时边界比转移更重要)

比如此题,最开始我并没有看出是区间$dp$,但我突然想起紫书上一道题,"割木棍"

仔细想想,几乎与此题一样

最开始,我定义$f[i,j]$表示端点$i$到端点$j$的最小代价,枚举切割点$k$

有

$$f[i,j] = underset{i<k<j}{min}left {f[i,k]+f[k,j]  ight }+(a[j]-a[i]+1)-1$$

但这样定义,$f$转移时就发生了重合,如下图

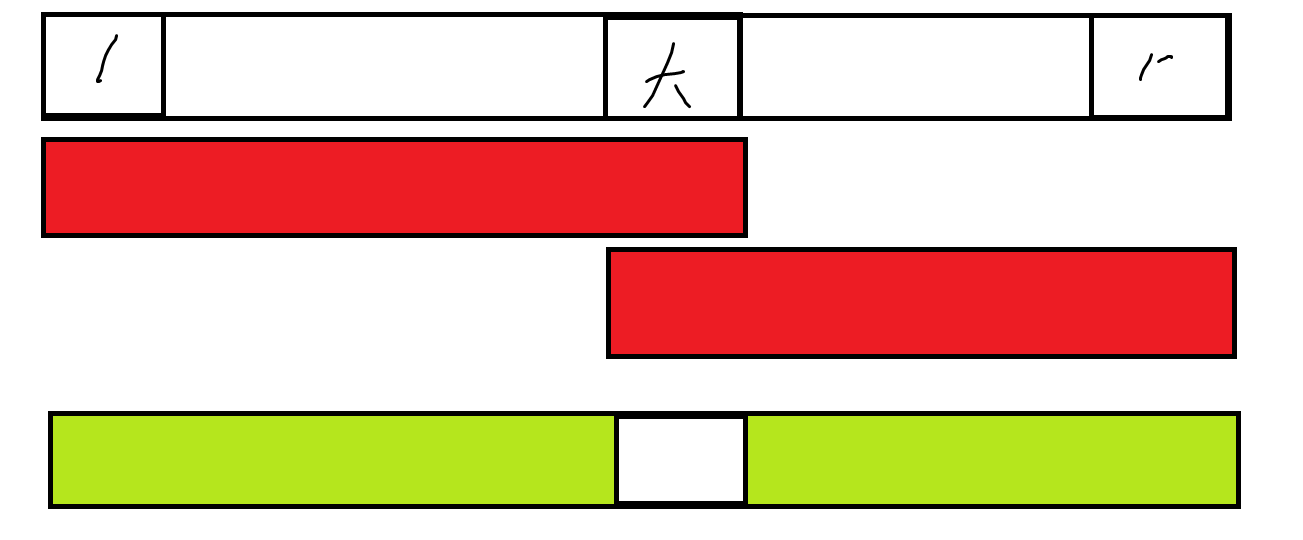
改变定义,令$f[i,j]$表示$i$到$j$(不包括端点$i$和$j$)的最小代价

有

$$f[i,j] = underset{i<k<j}{min}left {f[i,k]+f[k,j]  ight }+(a[j]-a[i]-1)-1$$

这样便是对的,如下图

代码如下

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define ll long long
//#include <stack>
using namespace std;

template <typename T> void in(T &x) {
    x = 0; T f = 1; char ch = getchar();
    while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
    while(isdigit(ch)) {x = 10*x + ch - '0'; ch = getchar();}
    x *= f;
}
//------------------------------------------------------------

const int N = 105;

int m,n,a[N],f[N][N];

int dp(int i,int j) {
    int &_f = f[i][j];
    if(_f) return _f;
    //if(i == j) return 0;
    if(i+1 == j) return 0;
    int tmp = 0x3f3f3f3f;
    for(int k = i+1;k <= j-1; ++k) tmp = min(tmp,dp(i,k)+dp(k,j));
    return _f = tmp+a[j]-a[i]-2;//-2
}

int main() {
    freopen("0.in","r",stdin);
    in(m); in(n);
    for(int i = 1;i <= n; ++i) in(a[i]);
    sort(a+1,a+n+1); a[0] = 0; a[n+1] = m+1;//0,m+1
    //memset(f,0x3f,sizeof(f));
    cout << dp(0,n+1);
    return 0;
}