题解 (by;zjvarphi)
状压 (dp),看到 (m) 的范围很小,考虑压 (m) 这一维。
一个状态 (st),其二进制位下的 1 代表的是当前一行划分成的每一段的开头。
合并的时候需要和上一行划分成的每一段合并,加上多出来的,放张图:
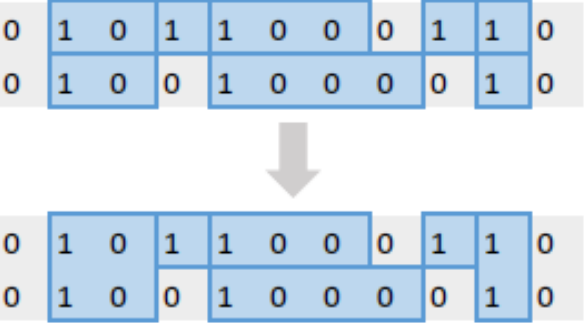
合并的时候只需要算新增的块就行。
细节不少,要提前预处理出所有合法的状态,具体看代码。
Code
#include<bits/stdc++.h>
#define ri signed
#define pd(i) ++i
#define bq(i) --i
#define func(x) std::function<x>
namespace IO{
char buf[1<<21],*p1=buf,*p2=buf;
#define gc() p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?(-1):*p1++
#define debug1(x) std::cerr << #x"=" << x << ' '
#define debug2(x) std::cerr << #x"=" << x << std::endl
#define Debug(x) assert(x)
struct nanfeng_stream{
template<typename T>inline nanfeng_stream &operator>>(T &x) {
bool f=false;x=0;char ch=gc();
while(!isdigit(ch)) f|=ch=='-',ch=gc();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=gc();
return x=f?-x:x,*this;
}
}cin;
}
using IO::cin;
namespace nanfeng{
#define pb emplace_back
#define FI FILE *IN
#define FO FILE *OUT
template<typename T>inline T cmax(T x,T y) {return x>y?x:y;}
template<typename T>inline T cmin(T x,T y) {return x>y?y:x;}
static const int N=107;
int mat[N],beg[N],dp[N][1<<9],n,m,S;
bool jud[9][9];
std::vector<int> st[N];
inline int main() {
FI=freopen("merging.in","r",stdin);
FO=freopen("merging.out","w",stdout);
cin >> n >> m;
S=(1<<m)-1;
for (ri i(1);i<=n;pd(i)) {
for (ri j(1);j<=m;pd(j)) {
int x;
cin >> x;
mat[i]|=x<<j-1;
if (j==1) {if (mat[i]) beg[i]=1;}
else if (x&&!((1<<j-2)&mat[i])) beg[i]|=1<<j-1;
}
for (ri j(0);j<=S;pd(j)) {
if ((j&mat[i])!=j||(beg[i]&j)!=beg[i]) continue;//当这个段的开头是所有1的子集,连续一段1的开头的集合的全集时才合法
st[i].pb(j);
}
}
st[0].pb(0);
memset(dp,0x3f,sizeof(dp));
dp[0][0]=0;
for (ri i(0);i<n;pd(i)) {
for (auto x:st[i]) {
memset(jud,false,sizeof(jud));
for (ri j(1);j<=m;pd(j))
if ((1<<j-1)&x) {
int nw=1,k=j;
for (j+=1;j<=m;pd(j))
if (!((1<<j-1)&x)&&((1<<j-1)&mat[i])) ++nw;
else break;
--j;
jud[k][nw]=true;
}
for (auto xx:st[i+1]) {
int sum=0,lst=0;
for (ri j(1);j<=m;pd(j))
if (((1<<j-1)&xx)) {
if (lst&&!jud[lst][j-lst]) ++sum;
lst=j;
} else if (!((1<<j-1)&mat[i+1])&&lst) {
if (!jud[lst][j-lst]) ++sum;
lst=0;
}
if (lst&&!jud[lst][m-lst+1]) ++sum;
dp[i+1][xx]=cmin(dp[i+1][xx],dp[i][x]+sum);
}
}
}
int ans=INT_MAX;
for (auto x:st[n]) ans=cmin(ans,dp[n][x]);
printf("%d
",ans);
return 0;
}
}
int main() {return nanfeng::main();}