利用问题的普遍性和特殊性来求解,
代码如下:
importunittest
fromdatetime importdatetime
classGetFreqNumbersFromList(unittest.TestCase):
defsetUp(self):
print("
")
self.start_time =datetime.now()
print(f"{self._testMethodName} start: {self.start_time}")
deftearDown(self):
self.end_time =datetime.now()
print(f"{self._testMethodName} end: {self.end_time}")
exec_time =(self.end_time -self.start_time).microseconds
print(f"{self._testMethodName} exec_time: {exec_time}")
defnormal_solution(self, _list, _debug=False):
"""
普遍性解法
利用字典记录每个元素出现的次数——然后找出元素出现次数超过数组长度一半的元素
普遍性解法针对任何次数的统计均适用而不光只是针对出现次数超过数组长度一半的情况
"""
_target =len(_list) //2
_dict ={}
for_member in_list:
if_member notin_dict:
_dict.setdefault(_member, 1)
else:
_dict[_member] +=1
_ret =[_member for_member in_dict if_dict[_member] > _target]
if_debug:
print(_ret)
return_ret
defspecific_solution(self, _list, _debug=False):
"""
特殊性解法
假设有两个元素出现的次数都超过数组长度一半就会得出两个元素出现的次数超出了数组长度的矛盾结果——所以超过数组长度一半的元素是唯一的
排序后在数组中间的一定是目标解
特殊性解法只能针对元素出现次数超过数组长度一半的情况
"""
_list.sort()
if_debug:
print(_list[len(_list) //2])
return_list[len(_list) //2]
deftest_normal_solution(self):
actual_result =self.normal_solution([2,2,2,2,2,2,1,1,1,1,1], False)
self.assertEqual(actual_result[0], 2)
deftest_specific_solution(self):
actual_result =self.specific_solution([2,2,2,2,2,2,1,1,1,1,1], False)
self.assertEqual(actual_result, 2)
if__name__ =="__main__":
# 找出出现次数超过数组长度一半的元素
suite =unittest.TestSuite()
suite.addTest(GetFreqNumbersFromList('test_normal_solution'))
suite.addTest(GetFreqNumbersFromList('test_specific_solution'))
runner =unittest.TextTestRunner()
runner.run(suite)
测试结果:
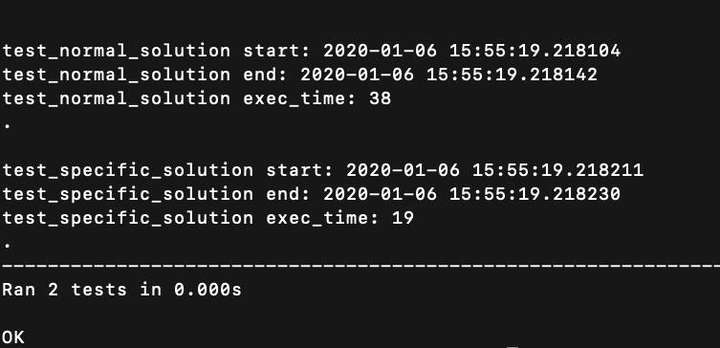
补充知识:Python 用积分思想计算圆周率
早上起来突然想求圆周率,1单位时圆的面积。
代码如下:
frommath importpow, sqrt
defcalc_circle_s_with(r, dy, x_slices):
x_from_start_to_cc =sqrt(1-pow(dy, 2))
dx =x_from_start_to_cc /x_slices
x_to_edge =1-x_from_start_to_cc
quarter_circle_s =0
whilex_to_edge < 1:
rect_s =dy *dx
quarter_circle_s +=rect_s
x_to_edge =x_to_edge +dx
dy =sqrt(1-pow((1-x_to_edge), 2))
circle_s =4*quarter_circle_s
print(circle_s)
calc_circle_s_with(1, 0.0001, 10000000)
运行结果接近3.1415926,dy传的越小,x_slices传的越大,就越接近。
半径为:1
初始小矩形到圆周的距离:1 - x_from_start_to_cc
其中dy代表四分之一圆中初始小矩形的高度,x_slices代表小矩形的宽度:(1 - x_from_start_to_cc) / x_slices
四分之一圆的面积积分为:quarter_circle_s
以上这篇Python 找出出现次数超过数组长度一半的元素实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持。
利用问题的普遍性和特殊性来求解,
代码如下:
测试结果:
补充知识:Python 用积分思想计算圆周率
早上起来突然想求圆周率,1单位时圆的面积。
代码如下:
运行结果接近3.1415926,dy传的越小,x_slices传的越大,就越接近。
半径为:1
初始小矩形到圆周的距离:1 - x_from_start_to_cc
其中dy代表四分之一圆中初始小矩形的高度,x_slices代表小矩形的宽度:(1 - x_from_start_to_cc) / x_slices
四分之一圆的面积积分为:quarter_circle_s
以上这篇Python 找出出现次数超过数组长度一半的元素实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持脚本之家。
