1，Euclidean distance
点p和点q的欧几米德距离就是线段pq的长度。
假设p的坐标为p=(p1,p1....pn) q的坐标为q=(q1,q2...qn)
那么p q间的距离:
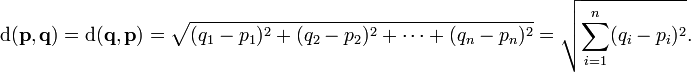
也可以用向量点积的形式表示为:
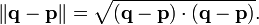
2,Pearson correlation coefficient
皮尔森相关系数就是概率论里的相关系数。
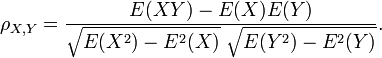
3,Tanimoto similarity
这是是看集体智慧编程的时候看到的，在第二章练习题中问何时Tanimoto similarity metric能够代替欧式距离和pearson系数？
Tanimoto的定义[1]：
if samples X and Y are bitmaps, 
is the ith bit of X, and 
are bitwise and, or operators respectively, then the similarity ratio 
is：
这个看起来不太容易，可是它和欧式距离一样，很容易理解。
举个例子，假设有3个特征A，B，C，D，三个样本X和Y和Z，其中X=（A：0,B:1,C:0,D:1）Y=（A：1,B:0,C:1,D:1） Z=（A：0，B：0，C：0，D：1），其中0，1表示有没有相应的特征
那么X，Y之间的相似性可以如下计算：T(X,Y)=(0+0+0+1)/(1+1+1+1)=0.25
X，Z之间的相似性可以如下计算： T(X,Z)=(0+0+0+1)/(0+1+0+1)=0.5
可以得出X与Z更相近。
Tanimoto similarity就是这么回事。
4,Manhattan distance
定义：The distance between two points measured along axes at right angles. In a plane with p1 at (x1, y1) and p2 at (x2, y2), the manhattan distance is |x1 - x2| + |y1 - y2|.
图中红色的线代表曼哈顿距离，绿色线代表欧式距离。
参考：
[1] http://en.wikipedia.org/wiki/Jaccard_index
http://en.wikipedia.org/wiki/Metric_(mathematics)
补充：发现一个很好的博客文章来讲这件事，在这里感谢作者
http://www.cnblogs.com/heaad/archive/2011/03/08/1977733.html
http://en.wikipedia.org/wiki/Metric_%28mathematics%29#Examples