题意:
找出N个不同的正数 (3 <= N <= 18) Ai (1 <= i <= N), 满足:
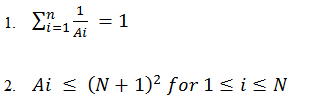
输出各个N个取值下的可能的解;
分析:
根据 1/(a * b) = 1/a(a + b) + 1/b(a + b) ,可以将一个可能的Ai 拆分成俩个
所有,由已知的一组当N等于3时的一组解{2,3,6},将其中一个可能的Ai拆分成俩个。
再由N等于4时的解求出N等于5时的解,以此类推;
#include<iostream>
#include<string.h>
#include<algorithm>
using namespace std;
int a[20],mark[400];
int main()
{
printf("2 3 6\n");
a[0]=2;a[1]=3;a[2]=6;
int num=3;
for(int i=4;i<=18;i++)
{
memset(mark,0,sizeof(mark));
for(int j=0;j<num;j++)
mark[a[j]]=1;
int flag=0;
for(int j=0;j<num ;j++){
for(int k=2;k*k<a[j];k++)
if(a[j]%k==0)//a[j]可以拆分成俩个数的乘积
{
int v=a[j]/k,w=k;
int p=v*(v+w),q=w*(v+w);
if(q>(i+1)*(i+1) || p>(i+1)*(i+1))continue;
if(mark[p]|| mark[q])continue;
mark[p]=1;mark[q]=1;mark[a[j]]=0;//将1/a[j]拆分成了1/p + 1/q
flag=1;break;//只需将一个拆分,所以找到一个可拆的即可退出
}
if(flag) break;
}
num=0;
for(int j=2;j<=(i+1)*(i+1);j++)
if(mark[j]) a[num++]=j;
sort(a,a+num);
for(int j=0;j<num-1;j++)
printf("%d ",a[j]);
printf("%d\n",a[num-1]);
}
return 0;
}