原论文:Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition https://arxiv.org/abs/1406.4729
综述
在R-CNN出来之后,卷积神经网络都要求输入固定的图像尺寸(比如224×224),而卷积层对与输入的尺寸是不敏感的,只是一种滑动滤波,输入的尺寸大输出的特征图就大,之所以限制喂入的卷积层图片尺寸是因为若干卷积层之后会接入全连接层(Fully connected layer),全连接层是要求有固定的特征图输入的,反推若干层前的卷积层就需要固定尺寸的土拍你输入。
论文中提出的“空间金字塔池化”(spatial pyramid pooling)的池化策略,可以有效消除上述限制。SPP-net结构能够产生固定大小的特征表示(fixed-length representation),而不关心输入图像的尺寸或比例。用SPP-net,我们只需要从整张图片计算一次特征图(feature map),然后对任意尺寸的区域(子图像)进行特征池化,以产生一个固定尺寸的表示(representation)用于训练检测器(detectors)。 这个方法避免了反复计算卷积特征。
SSP-Net
算法过程:
1.将经过SS处理后(含有2k个region proposal)的整幅图像输入CNNs,不需要对图像中的每一个proposal进行训练,然后得到整个featuremap,大大减少了计算proposal的特征时候的运算开销。为什么不用训练呢?原来是输入的proposal边界框位置与featuremap对应的边界框位置是线性的! a.取得ROI(region proposal)中心点位置(x,y) b.则对应的feature map上的边框左上角点为$lfloor x / S floor+1$,右下角点为$lfloor x / S floor-1$
省了很多计算有木有,对于每一副图像不需要训练CNN网络多次。只需要训练一次CNN,从特征图中得到候选窗口。
2.通过SS等方法得到的Region proposal(candidate windows)不再需要进行crop/wrap了,对比RCNN再喂入卷积层时需要映射到相同大小,因为convolution layer和Pooling layer并没有对图像尺寸大小的约束,而是在FC层有要求,该论文在FC层之前在最后的卷积层之后pool5层采用SSP,替代常规的Pooling,这也是该论文的其创新点。
spatial pyramid pooling(SPP)金字塔层
SSP层是对于卷积得到的N个feature maps进行多次池化操作, 并且池化核的大小逐渐增大, 这会导致着池化的输出逐渐减小,(像金字塔形状一样) 将这些池化后的输出合并起来, 作为FC的输入, 以此来解决FC要求的输入必须要一致的问题.
SPP层原理如下所所示,假定CNN层得到的特征图大小为a×a(比如13×13,随输入图片大小而变化),设定的金字塔尺度为n×n bins(对于不同大小图片是固定的),那么SPP层采用一种滑动窗口池化,窗口大小win_size=⌈a/n⌉,步为stride=⌊a/n⌋,采用max pooling,本质上将特征图均分为n×n个子区域,然后对各个子区域max pooling,这样不论输入图片大小,经过SPP层之后得到是固定大小的特征。一般设置多个金字塔级别,文中使用了4×4,2×2和1×1三个尺度。每个金字塔都得一个特征,将它们连接在一起送入后面的全连接层即可,这样就解决了变大小图片输入的问题了。
论文作者说 Multi-level pooling has been shown to be robust to object deformations,It is worth noticing that the gain of multi-level pooling is not simply due to more parameters; rather, it is because the multi-level pooling is robust to the variance in object deformations and spatial layout. 即 这种机制下会对目标的形变问题有很好的健壮性. 在我的理解下, 因为采用了这种多级的pooling操作, 所以在一定程度上, 在训练的过程中让网络学习到了在小范围和大范围下的形变下, 仍然能采样到标志性的特征.
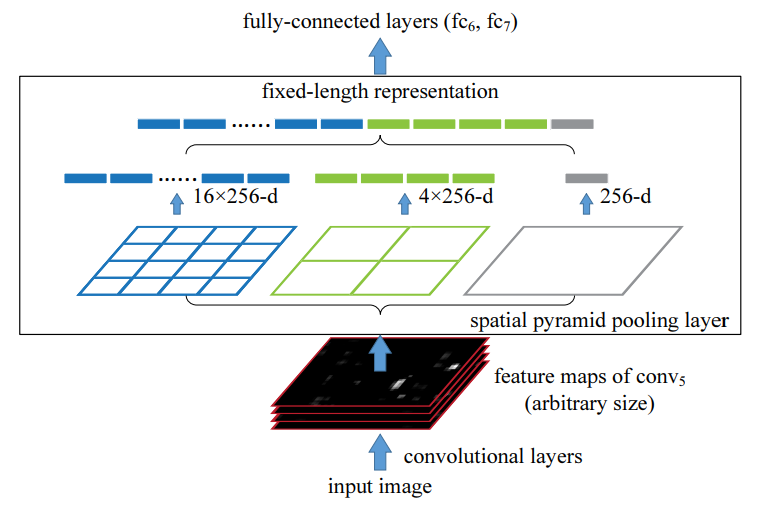
黑色图片代表卷积层之后的特征图,随后我们以不同大小的块来提取特征,分别是4 * 4,2 * 2,1 * 1,将这三张网格放到下面这张特征图上,就可以得到16+4+1=21种不同的块(Spatial bins)。我们从这21个块中,每个块提取出一个特征,这样刚好就是我们要提取的21维特征向量。这种以不同的大小格子的组合方式来池化的过程就是空间金字塔池化(SSP)。
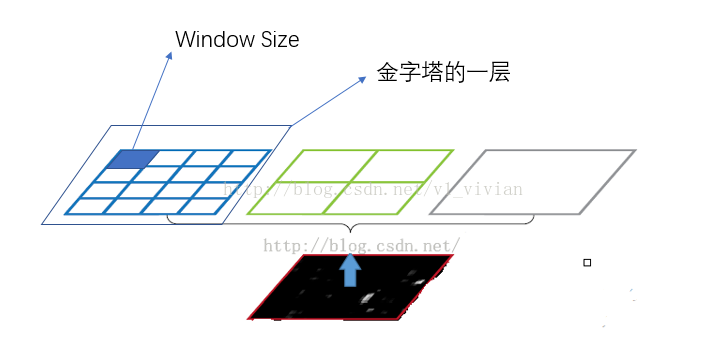
Conv5计算出的feature map也是任意大小的,现在经过SPP之后,就可以变成固定大小的输出了,以上图为例,一共可以输出(16+4+1)*256的特征
金字塔池化的意义是什么?
总结而言,当网络输入的是一张任意大小的图片,这个时候我们可以一直进行卷积、池化,直到网络的倒数几层的时候,也就是我们即将与全连接层连接的时候,就要使用金字塔池化,使得任意大小的特征图都能够转换成固定大小的特征向量,这就是空间金字塔池化的意义(多尺度特征提取出固定大小的特征向量)。
网络训练阶段:
论文中将网络的训练分为两种:一种是single-size,一种是Multi-size。
a.single-size训练过程
理论上说,SPP-net支持直接以多尺度的原始图片作为输入后直接BP即可。实际上,caffe等实现中,为了计算的方便,GPU,CUDA等比较适合固定尺寸的输入,所以训练的时候输入是固定了尺度了的。以224*224的输入为例:
在conv5之后的特征图为:13x13(a*a)
金字塔层bins: n*n
将pooling层作为sliding window pooling。
windows_size=[a/n] 向上取整 , stride_size=[a/n]向下取整。
例如论文中给出的参数如下:

对于pool 3*3: sizeX=5 的计算公式是:[13/3]向上取整=5 ,stride = 4的计算公式是:[13/3]向下取整。如果输入改成180x180,这时候conv5出来的reponse map为10x10,类似的方法,能够得到新的pooling参数。
b.Multi-size训练过程
训练的时候,224x224的图片通过crop得到,180x180的图片通过缩放224x224的图片得到。之后,迭代训练,即用224的图片训练一个epoch,之后180的图片训练一个epoch,交替地进行。
两种尺度下,在SSP层后,输出的特征维度都是(9+4+1)x256,参数是共享的,之后接全连接层即可。
论文中说,这样训练的好处是可以更快的收敛。
Mapping a Window to Feature Maps
我们知道,在原图中的proposal,经过多层卷积之后,位置还是相对于原图不变的(如下图所示),那现在需要解决的问题就是,如何能够将原图上的proposal,映射到卷积之后得到的特征图上,因为在此之后我们要对proposal进行金字塔池化。

对于映射关系,论文中给出了一个公式:
假设($x^{prime}$,$y^{prime}$)表示特征图上的坐标点,坐标点(x,y)表示原输入图片上的点,那么它们之间有如下转换关系,这种映射关心与网络结构有关: (x,y)=(S*x’,S*y’)
反过来,我们希望通过(x,y)坐标求解($x^{prime}$,$y^{prime}$),那么计算公式如下:
Left 、Top $x^{prime}=lfloor x / S floor+1$
Right 、Bottom $x^{prime}=lfloor x / S floor-1$
其中S就是CNN中所有的strides的乘积,包含了池化、卷积的stride
比如,对于下图的集中网络结构,S的计算如下:
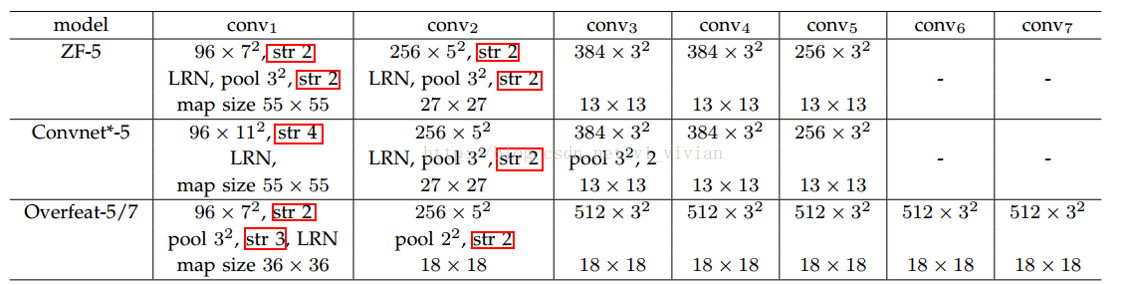
论文中使用的是 ZF-5模型: S=2*2*2*2=16
对于 Overfeat-5/7模型: S =2*3*2 =12
检测算法
对于检测算法,论文中是这样做到:使用ss生成~2k个候选框,缩放图像min(w,h)=s之后提取特征,每个候选框使用一个4层的空间金字塔池化特征,网络使用的是ZF-5的SPPNet形式。之后将12800d的特征输入全连接层,SVM的输入为全连接层的输出。
这个算法可以应用到多尺度的特征提取:先将图片resize到五个尺度:480,576,688,864,1200,加自己6个。然后在map window to feature map一步中,选择ROI框尺度在{6个尺度}中大小最接近224x224的那个尺度下的feature maps中提取对应的roi feature。这样做可以提高系统的准确率。
最后是SSP-Net的完整网络结构图
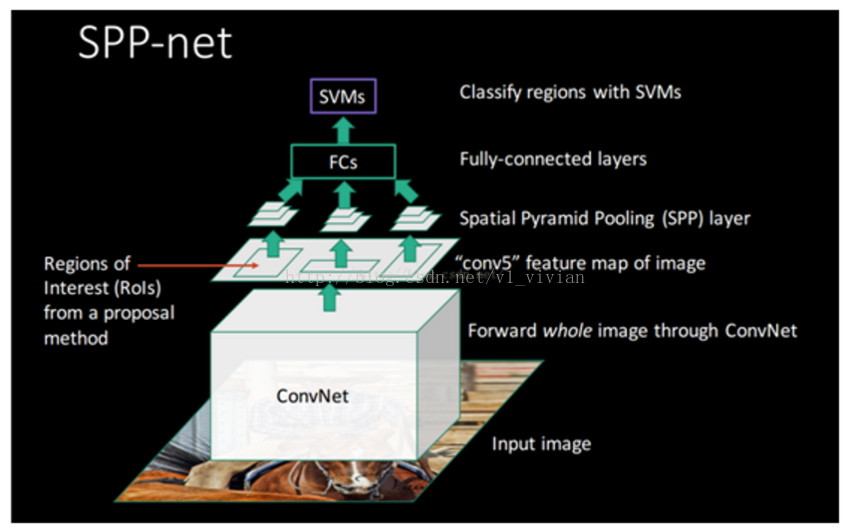
Reference
[2] https://baike.baidu.com/item/SPP-Net/22701886?fr=aladdin
[3] https://blog.csdn.net/programmingfool5/article/details/82667581