从TensorRT看INT8量化原理

本篇文章授权转载于大神arleyzhang的《TensorRT(5)-INT8校准原理》https://arleyzhang.github.io/articles/923e2c40/，支持原创请查看原文。

另附GTC 2017，Szymon Migacz 的PPT 

Low Precision Inference

现有的深度学习框架 比如：TensorFlow，pytorch，Caffe， MixNet等，在训练一个深度神经网络时，往往都会使用 float 32（Full Precise ，简称FP32）的数据精度来表示，权值、偏置、激活值等。但是如果一个网络很深的话，比如像VGG，ResNet这种，网络参数是极其多的，计算量就更多了（比如VGG 19.6 billion FLOPS, ResNet-152 11.3 billion FLOPS）。如此多的计算量，如果中间值都使用 FP 32的精度来计算的话，势必会很费时间。而这对于嵌入式设备或者移动设备来说，简直就是噩梦，因为他们的计算能力和内存数量是不能与PC相比的。

因此解决此问题的方法之一就是在部署推理时（inference）使用低精度数据，比如INT8。除此之外，当然还有模型压缩之类的方法，不过此处不做探究。注意此处只是针对 推理阶段，训练时仍然使用 FP32的精度。

从经验上来分析一下低精度推理的可行性：

实际上有些人认为，即便在推理时使用低精度的数据（比如INT8），在提升速度的同时，也并不会造成太大的精度损失，比如 Why are Eight Bits Enough for Deep Neural Networks? 以及Low Precision Inference with TensorRT 这两篇博文。

文章的作者认为网络在训练的过程中学习到了数据样本的模式可分性，同时由于数据中存在的噪声，使得网络具有较强的鲁棒性，也就是说在输入样本中做轻微的变动并不会过多的影响结果性能。与图像上目标间的位置，姿态，角度等的变化程度相比，这些噪声引进的变动只是很少的一部分，但实际上这些噪声引进的变动同样会使各个层的激活值输出发生变动，然而却对结果影响不大，也就是说训练好的网络对这些噪声具有一定的容忍度（tolerance ）。

正是由于在训练过程中使用高精度（FP32）的数值表示，才使得网络具有一定的容忍度。训练时使用高精度的数值表示，可以使得网络以很小的计算量修正参数，这在网络最后收敛的时候是很重要的，因为收敛的时候要求修正量很小很小（一般训练初始 阶段学习率稍大，越往后学习率越小）。

那么如果使用低精度的数据来表示网络参数以及中间值的话，势必会存在误差，这个误差某种程度上可以认为是一种噪声。那也就是说，使用低精度数据引进的差异是在网络的容忍度之内的，所以对结果不会产生太大影响。

以上分析都是基于经验的，理论上的分析比较少，不过文章提到了两篇 paper，如下：

• Improving the speed of neural networks on CPUs
• Training deep neural networks with low precision multiplications

这里不对这两篇paper做探究。

TensorRT 的INT8模式只支持计算能力为6.1的GPU（Compute Capability 6.1 ），比如： GP102 (Tesla P40 and NVIDIA Titan X), GP104 (Tesla P4), and GP106 GPUs，主要根源是这些GPU支持 DP4A硬件指令。DP4A下面会稍微介绍一下。

TensorRT INT8 Inference

首先看一下不同精度的动态范围:

	动态范围	最小正数
FP32	−3.4×1038 +3.4×1038−3.4×1038 +3.4×1038	1.4×10−451.4×10−45
FP16	−65504 +65504−65504 +65504	5.96×10−85.96×10−8
INT8	−128 +127−128 +127	11

实际上将FP32的精度降为INT8还是比较具有挑战性的。注：python的float类型式FP64的。

Quantization

将FP32降为INT8的过程相当于信息再编码（re-encoding information ），就是原来使用32bit来表示一个tensor，现在使用8bit来表示一个tensor，还要求精度不能下降太多。

将FP32转换为 INT8的操作需要针对每一层的输入张量（tensor）和 网络学习到的参数（learned parameters）进行。

首先能想到的最简单的映射方式就是线性映射（或称线性量化，linear quantization）, 就是说映射前后的关系满足下式：

$FP32 quad Tensor (T)=scale\_factor(sf) * 8-bit Tensor(t)+FP32\_bias (b)$

试验证明，偏置实际上是不需要的，因此去掉偏置，也就是

$T=sf * t$

$sf$是每一层上每一个tensor的换算系数或称比例因子（scaling factor），因此现在的问题就变成了如何确定比例因子。然后最简单的方法是下图这样的:

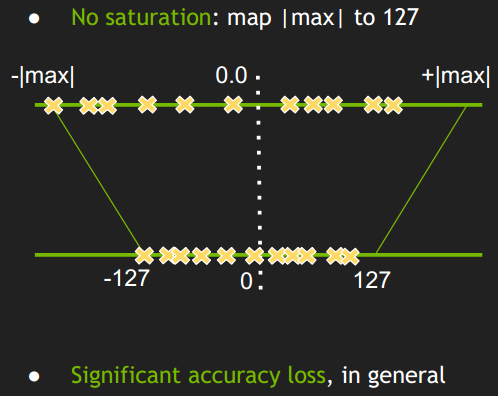
• 简单的将一个tensor 中的 -|max| 和 |max| FP32 value 映射为 -127 和 127 ，中间值按照线性关系进行映射。
• 称这种映射关系为不饱和的（No saturation ），对称的。

但是试验结果显示这样做会导致比较大的精度损失。

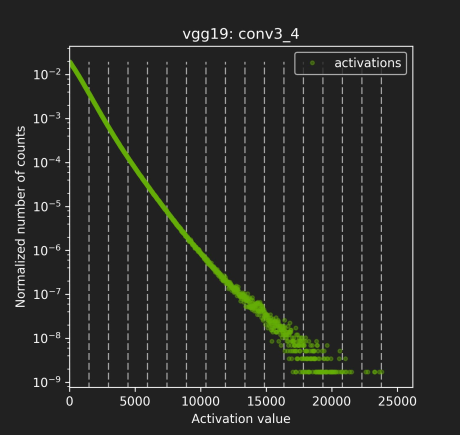
下面这张图展示的是不同网络结构的不同layer的激活值分布，有卷积层，有池化层，他们之间的分布很不一样，因此合理的 量化方式 应该适用于不同的激活值分布，并且减小 信息损失。因为从FP32到INT8其实就是一种信息再编码的过程

笔者理解的直接使用线性量化的方式导致精度损失比较大的原因是：

• 上图是一些网络模型中间层的 激活值统计，横坐标是激活值，纵坐标是统计数量的归一化表示，这里是归一化表示，不是绝对数值统计；
• 这个激活值统计 针对的是一批图片，不同的图片输出的激活值不完全相同。所以图上并不是一条曲线而是多条曲线（一张图片对应一条曲线，或者称为散点图更好一点），只不过前面一部分重复在一块了（红色虚线圈起来的部分），说明对于不同图片生成的大部分激活值其分布是相似的；但是在激活值比较大时（红色实线圈起来的部分），曲线不重复了，一个激活值对应多个不同的统计量，这时的激活值分布就比较乱了。
• 后面这一部分在整个层中是占少数的（占比很小，比如10^-9, 10^-7, 10^-3），因此后面这一段完全可以不考虑到映射关系中去，保留激活值分布的主方向。开始我以为网络之所以能把不同类别的图片分开是由于后面实线部分的差异导致的，后来想了一下：这个并不包含空间位置的分布，只是数值上的分布，所以后面的应该对结果影响不大。

因此TensorRT的做法是:

• 这种做法不是将 ±|max| 映射为 ±127，而是存在一个 阈值 |T| ，将 ±|T| 映射为±127，显然这里 |T|<|max|。
• 超出 阈值 ±|T| 外的直接映射为阈值 ±127。比如上图中的三个红色点，直接映射为-127。
• 称这种映射关系为饱和的（Saturate ），不对称的。
• 只要 阈值 选取得当，就能将分布散乱的较大的激活值舍弃掉，也就有可能使精度损失不至于降低太多。

网络的前向计算涉及到两部分数值：权值和激活值（weights 和activation，二者要做乘法运算），Szymon Migacz 也提到他们曾经做过实验，说对weights 做saturation （饱和量化）没有什么变化，因此 对于weights的int8量化就使用的是不饱和的方式；而对activation做saturation就有比较显著的性能提升，因此对activation使用的是饱和的量化方式。

那现在的问题是 如何确定|T|？我们来思考一下，现在有一个FP32的tensor，FP32肯定是能够表达这个tensor的最佳分布。现在我们要用一个不同的分布（INT8）来表达这个tensor，这个 INT8 分布不是一个最佳的分布。饱和的INT8分布由于阈值 |T|的取值会有很多种情况（128−|max|），其中肯定有一种情况是相对其他最接近FP32的，我们就是要把这种情况找出来。

既然如此，我们就需要一个衡量指标来衡量不同的 INT8 分布与原来的FP3F2分布之间的差异程度。这个衡量指标就是 相对熵（relative entropy），又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。叫法实在太多了，最常见的就是相对熵。跟交叉熵也是有关系的。

• 假设我们要给一个信息进行完美编码，那么最短平均编码长度就是信息熵。

• 如果编码方案不一定完美（由于对概率分布的估计不一定正确），这时的平均编码长度就是交叉熵。

  平均编码长度 = 最短平均编码长度 + 一个增量

  交叉熵在深度学习中广泛使用，衡量了测试集标签分布和模型预测分布之间的差异程度。

• 编码方法不一定完美时，平均编码长度相对于最小值的增加量（即上面那个增量）是相对熵。

即 交叉熵=信息熵+相对熵

对于分类，因为是离散的，对于离散型随机变量，信息熵公式如下：

$H(p)=H(X)=E_{x sim p(x)} [-logp(x)]=- sum_{i=1}^{n} p(x)log p(x)$

对于连续型随机变量，信息熵公式如下：

$H(p)=H(X)=E_{x sim p(x)}[-logp(x)]=- int p(x)log p(x)dx$

通俗的理解 信息熵，交叉熵，相对熵，参考：知乎：如何通俗的解释交叉熵与相对熵?

如何理解信息熵用来表示最短平均编码长度，参考： 如何理解用信息熵来表示最短的平均编码长度

详细的不说了，请看参考链接。

在这里，FP32的tensor就是我们要表达的信息量，FP32也是最佳分布（可以认为最短编码长度32bit），现在要做的是使用INT8 来编码FP32的信息，同时要求INT8编码后差异尽可能最小。考虑两个分布 P（FP32）、Q（INT8）KL散度计算如下：

$D_{KL}(p||q)= sum_{i=1}^{N} [p(x_{i})log p(x_{i})-p(x_{i})log q(x_{i})]= sum_{i=1}^{N} p(x_{i})log frac{p(x_{i})}{q(x_{i})}$

P，Q分别称为 reference_distribution、 quantize _distribution

实际上这里也说明了每一层的tensor 的 |T| 值都是不一样的。

确定每一层的 |T|值的过程称为 校准（Calibration ）。

Calibration

上面已经说了 KL散度越小代表 INT8编码后的信息损失越少。这一节来看看如何根据KL散度寻找最佳INT8分布。其实前面我们也已经提到了，如果要让最后的精度损失不大，是要考虑一些先验知识的，这个先验知识就是每一层在 FP32精度下的激活值分布，只有根据这个才能找到更加合理的 阈值|T|。也就是说首先得有一个以FP32精度训练好的模型。基本上现有的深度学习框架都是默认 FP32精度的，有些模型还支持FP16精度训练，貌似 Caffe2和MXNet是支持FP16的，其他的不太清楚。所以基本上只要没有特别设定，训练出来的模型肯定是 FP32 的。

那激活值分布如何得到？难道我们要将FP32的模型先在所有的测试集（或验证集）上跑一边记录下每一层的FP32激活值，然后再去推断 |T|?

这里的做法是 从验证集 选取一个子集作为校准集（Calibration Dataset ），校准集应该具有代表性，多样性，最好是验证集的一个子集，不应该只是分类类别的一小部分。激活值分布就是从校准集中得到的。

按照NVIDIA 官方的说法：

Note: The calibration set must be representative of the input provided to TensorRT at runtime; for example, for image classification networks, it should not consist of images from just a small subset of categories. For ImageNet networks, around 500 calibration images is adequate.

对于ImageNet 数据集来说 校准集大小一般500张图片就够了（Szymon Migacz的演讲说用1000张），这里有点怀疑也有点震惊，没想到 ImageNet 1000个分类，100多万张图片，500张就够了，不过从2.5节的图表中的结果可以看出500张确实够了。

然后要做的是：

• 首先在 校准集上 进行 FP32 inference 推理；
• 对于网络的每一层（遍历）：
  • 收集这一层的激活值，并做 直方图（histograms ），分成几个组别（bins）（官方给的一个说明使用的是2048组），分组是为了下面遍历 |T| 时，减少遍历次数；
  • 对于不同的 阈值 |T| 进行遍历，因为这里 |T|的取值肯定在 第128-2047 组之间，所以就选取每组的中间值进行遍历；
    • 选取使得 KL_divergence(ref_distr, quant_distr) 取得最小值的 |T|。
• 返回一系列 |T|值，每一层都有一个 |T|。创建 CalibrationTable 。

上面解释一下：假设 最后 使得 KL散度最小的|T|值是第200组的中间值，那么就把原来 第 0-200组的 数值线性映射到 0-128之间，超出范围的直接映射到128

 校准的过程可以参考一下这个：https://www.jianshu.com/p/43318a3dc715 , 这篇文章提供了一个详细的根据KL散度来将原始信息进行编码的例子，包括直方图的使用。跟这里的校准过程极为相像。

下面是一个官方 GTC2017 PPT 中给的校准的伪代码：

//首先分成 2048个组，每组包含多个数值（基本都是小数）
Input: FP32 histogram H with 2048 bins: bin[ 0 ], …, bin[ 2047 ] 
  
For i in range( 128 , 2048 ): // |T|的取值肯定在 第128-2047 组之间,取每组的中点
    reference_distribution_P = [ bin[ 0 ] , ..., bin[ i-1 ] ] // 选取前 i 组构成P，i>=128
    outliers_count = sum( bin[ i ] , bin[ i+1 ] , … , bin[ 2047 ] ) //边界外的组
    reference_distribution_P[ i-1 ] += outliers_count //边界外的组加到边界P[i-1]上，没有直接丢掉
    P /= sum(P) // 归一化
      
    // 将前面的P（包含i个组，i>=128），映射到 0-128 上，映射后的称为Q，Q包含128个组，
    // 一个整数是一组
    candidate_distribution_Q = quantize [ bin[ 0 ], …, bin[ i-1 ] ] into 128 levels
    
    //这时的P（包含i个组，i>=128）和Q向量（包含128个组）的大小是不一样的，无法直接计算二者的KL散度
    //因此需要将Q扩展为 i 个组，以保证跟P大小一样
    expand candidate_distribution_Q to ‘ i ’ bins 
    
    Q /= sum(Q) // 归一化
    //计算P和Q的KL散度
    divergence[ i ] = KL_divergence( reference_distribution_P, candidate_distribution_Q)
End For
//找出 divergence[ i ] 最小的数值，假设 divergence[m] 最小，
//那么|T|=( m + 0.5 ) * ( width of a bin )
Find index ‘m’ for which divergence[ m ] is minimal
threshold = ( m + 0.5 ) * ( width of a bin )

解释一下第16行：

• 计算KL散度 KL_divergence(P, Q) 时，要求序列P和Q的长度一致，即 len(P) == len(Q)；
• Candidate_distribution_Q 是将 P 线性映射到 128个bins得到的，长度为128。而reference_distribution_P 包含 i （i>=128）个 bins （bin[0] - bin[i-1] ），二者长度不等；
• 需要将 candidate_distribution_Q 扩展回 i 个bins 然后才能与 i个bins 的 reference_distribution_P计算KL散度。

举个简单的栗子：

• 假设reference_distribution_P 包含 8 个bins（这里一个bin就只包含一个数据）:

  P = [ 1, 0, 2, 3, 5, 3, 1, 7]

• 我们想把它映射为 2 个bins，于是 4个一组合并：

  [1 + 0 + 2 + 3 , 5 + 3 + 1 + 7] = [6, 16]

• 然后要成比例的 扩展回到 8个组，保留原来是0的组：

  Q = [ 6/3, 0, 6/3, 6/3, 16/4, 16/4, 16/4, 16/4] = [ 2, 0, 2, 2, 4, 4, 4, 4]

• 然后对 P和Q进行标准化：

  P /= sum(P) 、Q /= sum(Q)

• 最后计算散度：

  result = KL_divergence(P, Q)

我们来看看 ResNet-152中 res4b30层校准前后的结果对比:

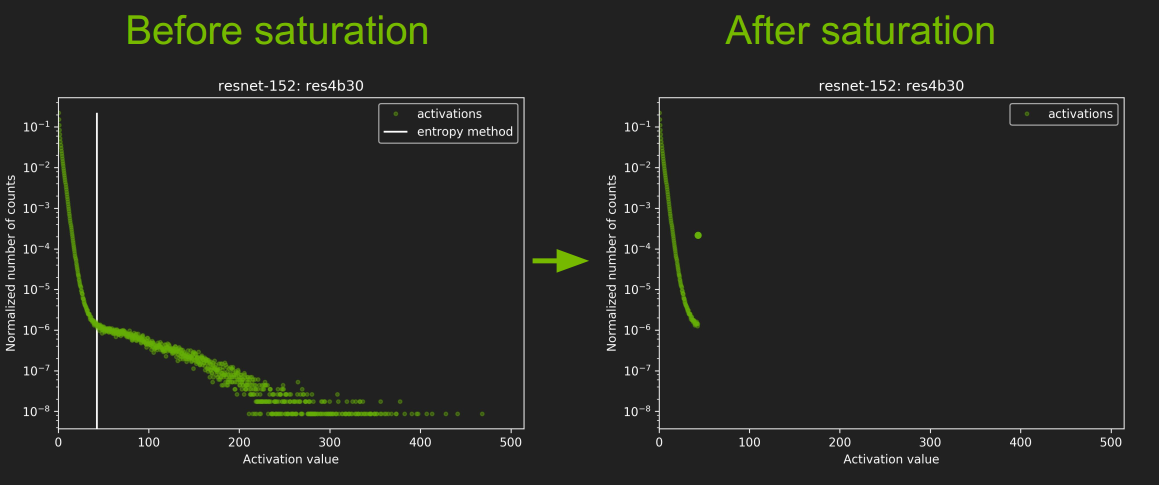
• 图中那个白线就是 |T|的取值，不过怎么还小于128了，有点没搞明白。

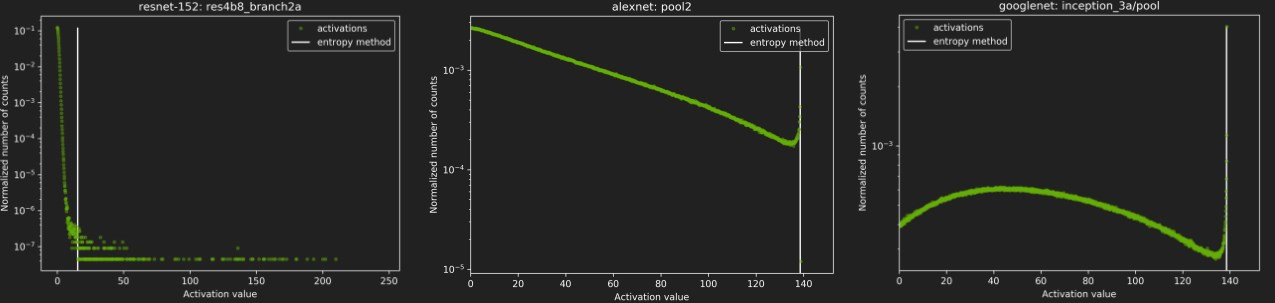
再看看其他几种网络的校准情况:

DP4A(Dot Product of 4 8-bits Accumulated to a 32-bit)

TensorRT 进行优化的方式是 DP4A (Dot Product of 4 8-bits Accumulated to a 32-bit)，如下图:

这是PASCAL 系列GPU的硬件指令，INT8卷积就是使用这种方式进行的卷积计算。

这个没搞太明白是怎么回事，参考这篇博客获取详细信息Mixed-Precision Programming with CUDA 8

下面是 官方 GTC2017 PPT 中给的INT8卷积计算的伪代码：

// I8 input tensors: I8_input, I8_weights, INT8输入tensor
// I8 output tensors: I8_output， INT8输出tensor
// F32 bias (original bias from the F32 model),FP32的偏置
// F32 scaling factors: input_scale, output_scale, weights_scale[K], 这个是前面说的缩放因子sf
I32_gemm_out = I8_input * I8_weights // Compute INT8 GEMM (DP4A)，卷积计算，INT32输出
F32_gemm_out = (float)I32_gemm_out // Cast I32 GEMM output to F32 float，强制转换为FP32
//前面计算I8_input * I8_weights时，总的缩放系数为 input_scale * weights_scale[K]
//但是输出的缩放系数为output_scale，所以为了保证缩放程度匹配，要将F32_gemm_out乘以 
//output_scale / (input_scale * weights_scale[ i ] )
  
// At this point we have F32_gemm_out which is scaled by ( input_scale * weights_scale[K] ),
// but to store the final result in int8 we need to have scale equal to "output_scale", so we have to rescale:
// (this multiplication is done in F32, *_gemm_out arrays are in NCHW format)
For i in 0, ... K-1:
rescaled_F32_gemm_out[ :, i, :, :] = F32_gemm_out[ :, i, :, :] * [ output_scale /(input_scale * weights_scale[ i ] ) ]
  
//将FP32精度的偏置 乘上缩放因子，加到前面的计算结果中
// Add bias, to perform addition we have to rescale original F32 bias so that it's scaled with "output_scale"
rescaled_F32_gemm_out _with_bias = rescaled_F32_gemm_out + output_scale * bias
//ReLU 激活
// Perform ReLU (in F32)
F32_result = ReLU(rescaled_F32_gemm_out _with_bias)
//重新转换为 INT8
// Convert to INT8 and save to global
I8_output = Saturate( Round_to_nearest_integer( F32_result ) )

它这个INT8卷积的计算是这样的，虽然输入的tensor已经降为 INT8，但是在卷积计算的时候用了DP4A的计算模式，卷积计算完之后是INT32的，然后又要转成 FP32，然后激活，最后再将FP32的转为INT8.

只知道这么计算会快很多，但不知道为什么，详情还是看Mixed-Precision Programming with CUDA 8 。

不过这个对于tensorRT的使用没啥影响，这个是很底层的东西，涉及到硬件优化。

Typical workflow in TensorRT

典型的工作流还是直接使用 GTC2017 PPT 原文说法吧：

• You will need:
  • Model trained in FP32.
  • Calibration dataset.
• TensorRT will:
  • Run inference in FP32 on calibration dataset.
  • Collect required statistics.
  • Run calibration algorithm → optimal scaling factors.
  • Quantize FP32 weights → INT8.
  • Generate “CalibrationTable” and INT8 execution engine.

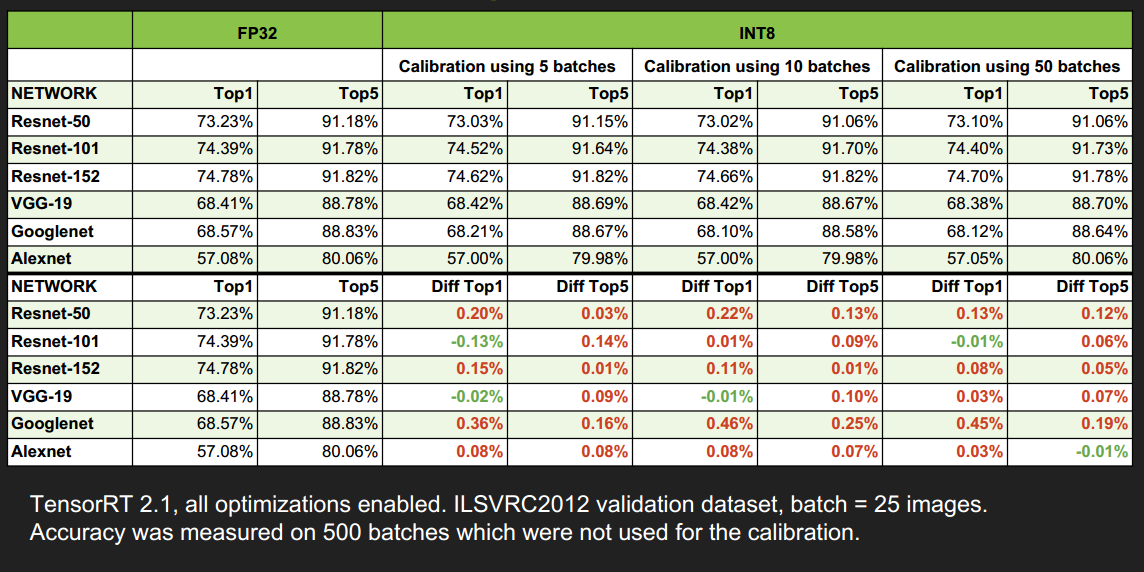
Results - Accuracy & Performance

精度并没有损失太多

 速度提升还蛮多的，尤其是当 batch_size 大于1时，提升更明显

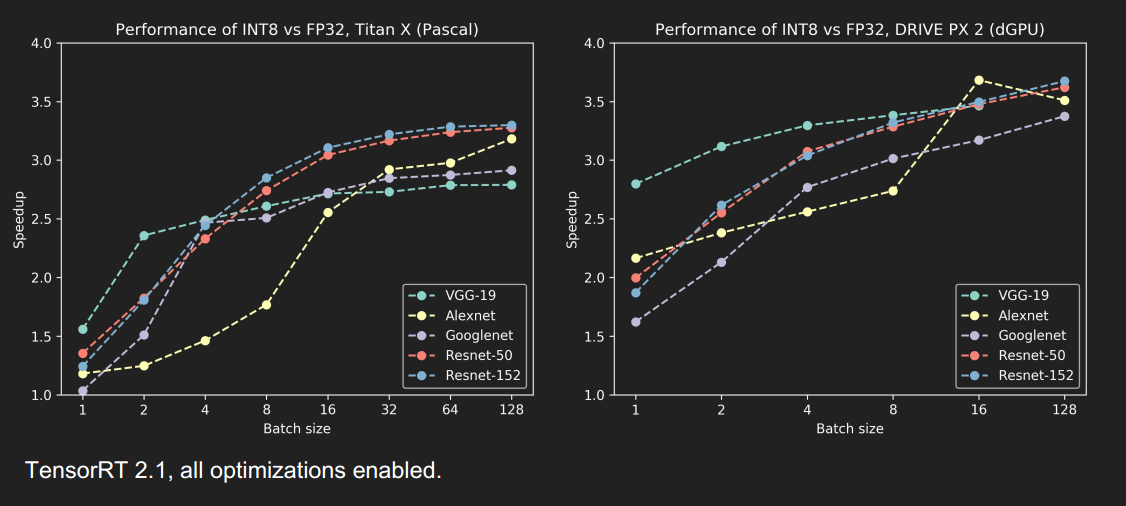
 TITAN X GPU优化效果

 DRIVE PX 2, dGPU 优化效果

Open challenges / improvements

一些开放式的提升和挑战：

• Unsigned int8 for activations after ReLU. 无符号 INT8 的映射。
• RNNs → open research problem. TensorRT 3.0开始已经支持RNN了。
• Fine tuning of saturation thresholds. 对阈值 |T|的 微调方法。
• Expose API for accepting custom, user provided scale factors. 开放API，使用户可以自定义 换算系数（比例因子）

这几个开放问题还是很值得研究的。

Conclusion

• 介绍了一种自动化，无参数的 FP32 到 INT8 的转换方法；
• 对称的，不饱和的线性量化，会导致精度损失较大；
• 通过最小化 KL散度来选择 饱和量化中的 阈值 |T|;
• FP32完全可以降低为INT8推理，精度几乎持平，速度有很大提升。

Reference

[1] https://arleyzhang.github.io/articles/923e2c40/