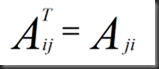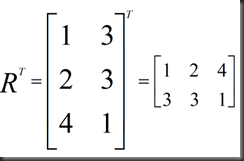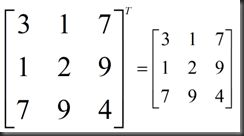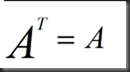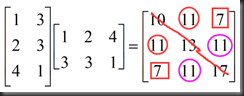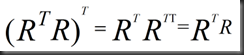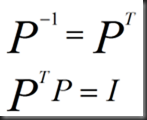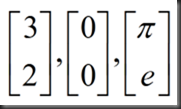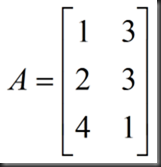Section 2.7 PA=LU
and Section 3.1 Vector Spaces and Subspaces
Transpose(转置)
example:
特殊情况,对称矩阵(symmetric matrices),例如:
思考:R^R(R的转置乘以R)有什么特殊的?
回答:always symmetric
why?
Permutation(置换)
P=execute row exchanges
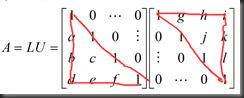
之前A=LU是建立在no row exchanges 的基础上的,但不可能每一个矩阵都是完美的,有些矩阵需要通过行变换处理,
即PA=LU (any invertible A)
P= indentity matrix with reordered rows
置换矩阵是重新排列了的单位矩阵
counts reorderings(counts all the n * n permutations : n!
性质:
Vector Spaces
Example:
R^2= all 2 dimensional real vectors = “x-y”plane,
R^3= all vectors with 3 component
R^n = all vectors with n component
思考:not a vector space? what’s the condition?
回答:向量空间必须对数乘和加法两种运算是封闭的(线性组合封闭)
比如说,二维平面子空间 line in R^2 through zero vector
总结:
subspaces of R^2: all of R^2(itself), any line through zero vector (L), zero vector only (Z)
subspaces of R^3: all of R^3(itself), any plane through zero vector (P), any line through zero vector (L), zero vector only (Z)
example:
cols in R^3, all their combinations form a subspace called column space, C(A)