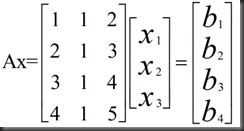Vector spaces and subspaces
Column space of A solving Ax=b
Null space of A
Vector space requirements v+w and cv are in the space
All combs cv+dw are in the space
向量空间对数乘和加法需要封闭
subspace of R^3:
Line( L) through zero vector is a subspace of R^3
Plane( P) through zero vector is a subspace of R^3
then we got 2 subspaces: P and L
P∪L means all vectors in P or L or both, this is not a subspace, 原因在于对加法不封闭,加和后所得的可能既不在P上,也不在L上
P∩L means all vectors in both P and L, this is a subspace, 交点为zero
Column space of A(列空间),记作C(A)
example:
 is a subspace of R^4, 记作 C ( A)
is a subspace of R^4, 记作 C ( A)
思考:Does Ax=b have a solution for every b? Which b’s allow this system to be solved?
回答:No. 4 equations, 3 unknowns, we can solve Ax=b exactly when b is in C( A)
接下来考虑nullspace of A: all solutions to Ax=0
now write some solutions, such as
观察规律可总结出一般形式
Check the solution to Ax=0 always give a subspace
If Av=0 and Aw=0, then A(v+w)=0, then A(12v)=0,即对加法和数乘都封闭
another example:
解中不包含zero vector,故不构成space,那么它的解是什么样的呢?
summary:
subspace:1、combination of several vectors
2、从方程组中通过让x满足特定条件