一、最小化误差函数拟合##
正则化( regularization )技术涉及到给误差函数增加一个惩罚项,使得系数不会达到很大的值。这种惩罚项最简单的形式采用所有系数的平方和的形式。这推导出了误差函数的修改后的形式:
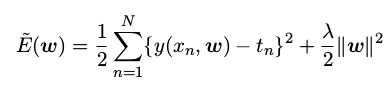
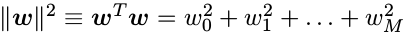
在效果上, λ 控制了模型的复杂性,因此决定了过拟合的程度。
二、贝叶斯曲线拟合##
1.正态分布( normal distribution )或者高斯分布( Gaussian distribution )###
对于一元实值变量 x ,高斯分布被定义为:
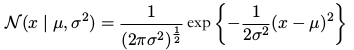
它由两个参数控制:(μ) ,被叫做均值( mean ),以及(σ^2) ,被叫做方差( variance )。方差的平方根,由 (σ) 给定,被叫做标准差( standard deviation )。方差的倒数,记作 (β = frac{1}{σ^2}) ,被叫做精度( precision )。
D 维向量 x 的高斯分布:
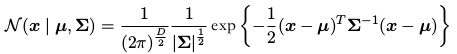
2.曲线拟合###
曲线拟合问题的目标是能够根据 N 个输入 (x = (x_1 , . . . , x_N )^T) 组成的数据集和它们对应的目标值 (t = (t_1 , . . . , t_N )^T) ,在给出输入变量 x 的新值的情况下,对目标变量 t 进行预测。
对应的 t 值服从高斯分布,分布的均值为 y(x, w) ,有:
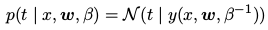
图形化表示:
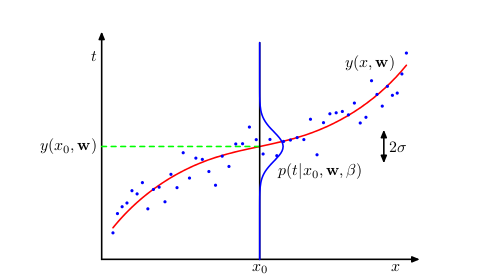
用训练数据$ {x, t}$ ,通过最大似然方法,来决定未知参数 w 和 β 的值,然函数为:
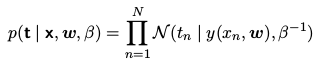
对数似然函数:
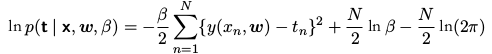
求其最大值就可以求得(w)。进一步确定精度参数 (β):