“大O记法”:对于单调的整数函数f(n),如果存在一个整数函数g(n)和常数c>0,使得对于充分大的n总有f(n)<=c*g(n),就说函数g(n)是f(n)的一个渐近函数(忽略常量因子),记为f(n)=O(g(n))。易见,f(n)=O(g(n))说明在n趋于无穷大的时候,函数f的增长速度受到函数g的约束。
假设存在函数g,使得算法A处理规模为n的问题实例所用的时间T(n)=O(g(n)),则称O(g(n))为算法A的渐近时间复杂度,简称时间复杂度
它表示随着问题规模的n的增大,算法的执行时间的增长率和f(n)的增长率相同,这称作算法的渐进时间复杂度,简称时间复杂度。而我们一般讨论的是最坏时间复杂度,这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的上界,分析最坏的情况以估算算法指向时间的一个上界。 时间复杂度的分析方法: 1、时间复杂度就是函数中基本操作所执行的次数 2、一般默认的是最坏时间复杂度,即分析最坏情况下所能执行的次数 3、忽略掉常数项 4、关注运行时间的增长趋势,关注函数式中增长最快的表达式,忽略系数 5、计算时间复杂度是估算随着n的增长函数执行次数的增长趋势 6、递归算法的时间复杂度为:递归总次数 * 每次递归中基本操作所执行的次数
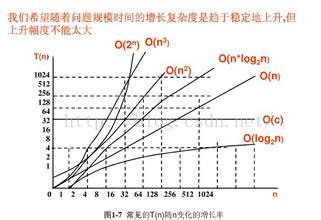
常量复杂度:O(l)
对数复杂度:O(log n)
线性复杂度:O(n)
平方复杂度:O(n2)
指数复杂度:O(2n)
空间复杂度:
算法的空间复杂度并不是计算实际占用的空间,而是计算整个算法的辅助空间单元的个数,与问题的规模没有关系。算法的空间复杂度S(n)定义为该算法所耗费空间的数量级。
S(n)=O(f(n)) 若算法执行时所需要的辅助空间相对于输入数据量n而言是一个常数,则称这个算法的辅助空间为O(1); 递归算法的空间复杂度:递归深度N*每次递归所要的辅助空间, 如果每次递归所需的辅助空间是常数,则递归的空间复杂度是 O(N).