第一次学习置换群这个东西。
这题需要利用Burnside定理。
即我们求出循环节为一(转完不变)的个数的平均数也就是等价类的个数。
定义:设G={a1,a2,…ag}是目标集[1,n]上的置换群。每个置换都写成不相交循环的乘积。 c1(ak) 是在置换ak 的作用下不动点的个数,也就是长度为1的循环的个数(其实就是被置换ak 置换过后位置不变的元素个数)。通过上述置换的变换操作后可以相等的元素属于同一个等价类。若G将[1,n]划分成L个等价类,则:
等价类个数为:
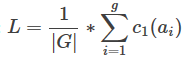
证明:http://blog.csdn.net/gengmingrui/article/details/50564027
这样我们就相当于求每一种置换有多少不同的使得转完后不变的方案数,利用01背包可求。
而转完不变的意思就是转完后颜色还是原来的颜色。
然后答案是在mod p意义下的所以要用逆元。
By:大奕哥
1 #include<bits/stdc++.h> 2 using namespace std; 3 int sr,sb,sg,m,p,n; 4 int e[75][75],size[75],f[75][75][75]; 5 bool v[75]; 6 int dp(int x) 7 { 8 memset(f,0,sizeof(f)); 9 memset(size,0,sizeof(size)); 10 memset(v,0,sizeof(v)); 11 int cnt=0; 12 for(int i=1;i<=n;++i) 13 { 14 if(v[i])continue; 15 cnt++;int p=e[x][i]; 16 while(!v[p])size[cnt]++,v[p]=1,p=e[x][p]; 17 } 18 f[0][0][0]=1; 19 for(int i=1;i<=cnt;++i) 20 for(int SR=sr;SR>=0;SR--) 21 for(int SB=sb;SB>=0;SB--) 22 for(int SG=sg;SG>=0;SG--) 23 { 24 if(SR>=size[i])f[SR][SB][SG]=(f[SR][SB][SG]+f[SR-size[i]][SB][SG])%p; 25 if(SB>=size[i])f[SR][SB][SG]=(f[SR][SB][SG]+f[SR][SB-size[i]][SG])%p; 26 if(SG>=size[i])f[SR][SB][SG]=(f[SR][SB][SG]+f[SR][SB][SG-size[i]])%p; 27 } 28 return f[sr][sb][sg]; 29 } 30 int quick_mod(int a,int b) 31 { 32 int ans=1; 33 while(b) 34 { 35 if(b&1)ans=ans*a%p; 36 a=a*a%p;b>>=1; 37 } 38 return ans; 39 } 40 int main() 41 { 42 scanf("%d%d%d%d%d",&sr,&sb,&sg,&m,&p);n=sb+sr+sg; 43 for(int i=1;i<=m;++i) 44 for(int j=1;j<=n;++j) 45 scanf("%d",&e[i][j]); 46 ++m;int ans=0; 47 for(int i=1;i<=n;++i)e[m][i]=i; 48 for(int i=1;i<=m;++i) 49 ans=(ans+dp(i))%p; 50 ans=(ans*quick_mod(m,p-2))%p; 51 printf("%d ",ans); 52 return 0; 53 }