Date:
Nov. 4, 2017
Problem:
https://leetcode.com/problems/largest-rectangle-in-histogram/description/
Description:
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
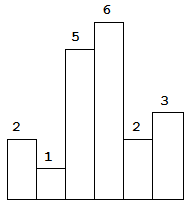
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3]

The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example:
Given heights = [2,1,5,6,2,3], return 10.
很容易想到暴力解法。遍历heights,对一个heights[i],向左寻找第一个l,使得heights[l] < heights[i],向右寻找第一个r,使得heights[r] < heights[i]。maxarea = max(maxarea, heights[i] * (r - l - 1))。这种解法的复杂度为O(N^2)。TLE。
对解法优化,对每一个i只向右检索,初始化height = heights[i],遇heights[j] < height结算,遇heights[j] = height记录,被记录的heights不需要再检查。结算后令height = heights[j],继续向右扫描。这种解法提供了非常好的优化,但是最坏复杂度仍为O(N^2)。遇到恶意输入[1, 2, 3, 4, ... , N],TLE。
研究两种稳定而性能优秀的算法。反思暴力解法,我们查找符合条件的r和l时不需要遍历数组,只需要研究之前的查找结果。用left_smaller[i]记录对i而言满足条件的l,初始化left_smaller[0] = -1。研究left_smaller[i]时,我们考虑一个回溯:
while temp >= 0 and heights[temp] >= heights[i]: temp = left_smaller[temp]
temp初始化为i - 1,回溯完成后令left_smaller[i] = temp。
这个回溯起到了非常良好的压缩路径的效果。考虑一颗这样的树,在根节点的父节点处设置哨兵-1,此外每个节点的父节点是它向左查找到的第一个l,使得heights[l] < heights[i]——我们把这一关系叫做A关系。我们正是用parent = left_smaller[son]来描述父子节点间的A关系。当我们向这棵树里放置新节点i时,用temp临时记录其可能的父节点。我们首先令temp = i - 1,很显然,当temp和i满足A关系时,我们可以放心地将i加入temp的子节点。但是,当height[temp] >= height[i],我们应该向上一级父节点查询它是否与新节点具有A关系。因为,对l = left_smaller[temp] + 1 ~ temp,height[l] >= height[temp] >= height[i],任意l都不可能是i的父节点。于是向树的根部回溯,直到temp与i满足A关系,我们将i加入temp的子节点。
研究right_smaller[i],依葫芦画瓢。
这一解法的复杂度为O(N)。
以下是submission:
1 class Solution: 2 def largestRectangleArea(self, heights): 3 length = len(heights) 4 left_smaller = [-1] * length 5 right_smaller = [length] * length 6 result = 0 7 for i in range(1, length): 8 temp = i - 1 9 while temp >= 0 and heights[temp] >= heights[i]: 10 temp = left_smaller[temp] 11 left_smaller[i] = temp 12 for i in range(length - 2, -1, -1): 13 temp = i + 1 14 while temp < length and heights[temp] >= heights[i]: 15 temp = right_smaller[temp] 16 right_smaller[i] = temp 17 for i in range(length): 18 result = max(result, heights[i] * (right_smaller[i] - left_smaller[i] - 1)) 19 return result
另一种解法,维护一个优美的栈,使得其中的元素总是升序。仍然从暴力解法的思路出发,对一个i,我们要计算与它相关的maxarea,只需要向左寻找第一个l,使得heights[l] < heights[i],向右寻找第一个r,使得heights[r] < heights[i]。换言之,我们只关心左侧第一个小于height[i]的l的坐标和右侧第一个小于height[i]的r的坐标。所以,当我们总是维护一个升序栈,当压入新元素r,使得height[r] < height[stack[i]]时,显然对于stack[i],我们总能找到height[r] < height[stack[i]],height[stack[i - 1]] < height[stack[i]]。此时我们结算stack[i]相关的maxarea,将其弹出,重复上述操作,直到栈恢复升序。如此,我们便在O(N)的时间内优雅地遍历了所有i的maxarea。
以下是submission。
1 class Solution: 2 def largestRectangleArea(self, heights): 3 stack = [-1] 4 rank = 0 5 result = 0 6 heights.append(0) 7 length = len(heights) 8 for i in range(length): 9 while rank > 0 and heights[i] <= heights[stack[rank]]: 10 result = max(result, heights[stack[rank]] * (i - stack[rank - 1] - 1)) 11 stack.pop() 12 rank -= 1 13 rank += 1 14 stack.append(i) 15 return result