网上有很多关于这个问题的解答,但好像都是正常坐标系下的,因为需求我改进一下,在屏幕坐标系的旋转。
参考:(有很详细的证明过程)
在平面中,一个点绕任意点旋转θ度后的点的坐标
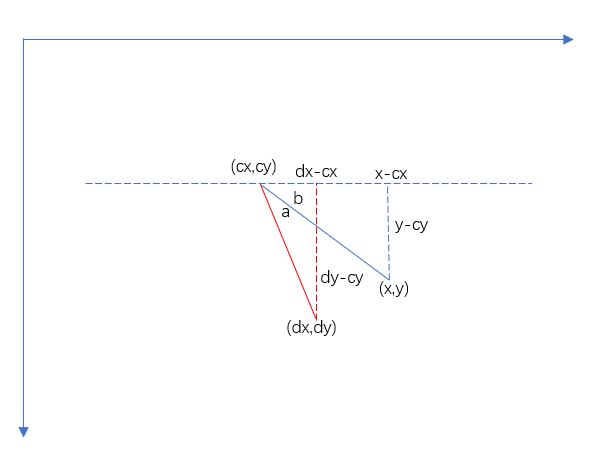
顺时针旋转
cos(a+b)=(dx-cx)/L
cos(b)=(x-cx)/L
sin(a+b)=(dy-y)/L
sin(b)=(y-cy)/L
(dx-cx)/(x-cx)=cos(a+b)/cos(b)
得到:dx=(x-cx)cos(a)-(y-cy)sina+cx
(dy-cy)/(y-cy)=sin(a+b)/sin(b)
得到:dy=(x-cx)sin(a)+(y-cy)cos(a)+cy
逆时针同样可以得到,只是稍微麻烦点
dx=(x-cx)cos(a)+(y-cy)sin(a)+cx
dy=(y-cy)cos(a)-(x-cx)sin(a)+cy