Clipper库中文文档详解
简介
Clipper Library(以下简称为Clipper库或ClipperLib或Clipper)提供了对线段和多边形的裁剪(Clipping)以及偏置(offseting)的功能
和其他的裁剪库相比,Clipper具有以下特征:
1. 它能够接受各类多边形输入,包含自交的多边形
2. 它支持多种填充规则(奇偶填充、非零填充、正填充、负填充)
3. 它相较于其他库效率极高
4. 它数值稳定(鲁棒性强),鲁棒性:https://baike.baidu.com/item/%E9%B2%81%E6%A3%92%E6%80%A7/832302?fr=aladdin
5. 它支持多边形和线段的偏置
6. 它对于商用以及免费软件来说都是免费的
术语:
裁剪(Clipping):通常是指在二维平面把一个图形在指定的矩形框以外的部分去除掉。在更广义的角度,指定的裁剪范围不一定是一个矩形,可以是各种各样的多边形,甚至是多个多边形;同样的,我们一般裁剪指的是形态学上的“求交”,在Clipper库中裁剪可以实现4中布尔运算(求交、求和、求异、求异或);
路径(Path):是指一系列的有序的点的集合,用来定义一个轮廓(Contour),这个轮廓既可以是代指一条线/开放路径(line/open path),也可以代指一个多边形/闭合轮廓(polygon/ closed path)
线(Line):与Polyline同义,代指一个具有两个点或以上点的开放路径
轮廓(Contour):与路径同义
孔洞/内轮廓(Hole):代指一个多边形内部表示该部分不属于该多边形的闭合区域:一个“内轮廓(Hole Polygon)”就是一个代指孔的外围点集的封闭路径
多边形填充规则(Polygon Filling Rule):即在一系列的闭合路径中,来定义哪些属于“内部”,哪些属于“外部”
预定义宏(Defines)
编译器预定义以下类型的宏:
use_int32:当启用32位精度,效率提升,但是使用范围缩小
use_xyz:添加一个Z位数据,对性能影响很小
use_lines:启用开放路径的裁剪;如果该功能关闭(默认开启),大约有一个小于5%的性能的提升
use_deprecated:确保代码与6.0版本以前的内容相兼容;该功能未来可能会删除
取整(Rounding)
通过使用一个整形数据,Clipper库已经能够避免因为数值稳定性造成的重大错误,关于数值取整问题和可能的解决方法如下:
首先要强调的是,取整导致点会对他们本来的理论坐标形成一定程序的偏移,但是结果的不精确性是可以通过正确的缩放来进行避免的;
Clipper库自身支持可以缩放到一个相对较高精度,它所支持的整形坐标值范围在±0x3FFFFFFFFFFFFFFF (± 4.6e+18)之间
另一个使用离散数据(相较于使用浮动类型数据)的隐患在于可能在极少数的情况下会造成小的自交情况在没有缩放的左侧图片中(这里单位为1像素),两个多边形的相交部分被用亮绿色标出;
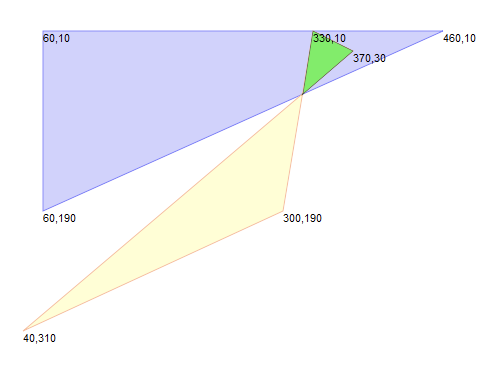
一个30倍放大的交点部分。下图显示该图其实有很小程度的自交情况,三个黑点表明了实际的交点情况(通过展示它们小数点部分);红色显示在取整之后交点的情况,会很容易观察到取整让方向变反并且引起了一定程度的小的自交;
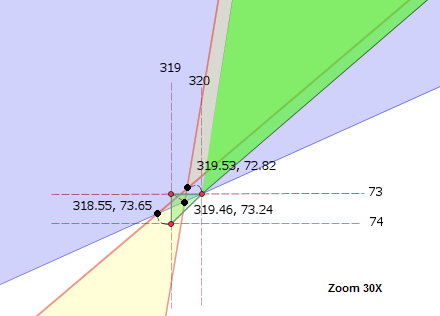
尽管这些小的自交是不常见的,如果这些被认为是有必要被考虑的,最好使用**CleanPolygon**的属性来对这种情况进行清除;(将Clipper对象的StrictlySimple属性设定为true同样会对这类自交产生影响但是小的多余的人为引起的错误方向的多边形仍然是不可避免的)
数据类型
cInt
cInt是Clipper库用来表示点坐标数据使用的,目前Clipper库使用整形数据代替浮点数据来保证数据的鲁棒性。
默认的cInt代表了一个有符号64位整形数据并且整个多边形的坐标范围可以达到±9.2e+18的范围内。这容纳了整个浮点数坐标可以使其精度得到最完整的保留。但是,如果坐标范围可以被控制在 ± 3.0e+9之内,那么通过避免了大数的运算,可以得到大约百分之十的效率提升。如果预编译器定义了use_int32,则效率可以更高。
IntPoint
整形点数据结构用来代表Clipper库中相关的所有点;Clipper库刻意选择了整形存储类型类保证数值稳定。
一系列的IntPoint被保存在Path结构中,构成了一个轮廓。
在版本6.0以上,IntPoint现在可以拥有第三个成员“Z”,这可以通过预编译器中定义“use_xyz”来实现,当Z轴数据也被加入时,它的值也会被考虑进裁剪的行为中去,但是,在那些没有对应的Z值交点处,该值会被设定为0,除非用户提供了回调函数。
用户如果希望使用浮点数进行Clip,那么必须手动的进行正确的对浮点数进行缩放为IntPoint,在使用Clipper进行处理。
Path
这个结构包含一系列的整形数据点来定义一个单独的轮廓;路径由两个及以上的点数据组成,并且可以是开放的,当它闭合的时候也可以代表多边形(Polygon);路径的开放与否是由其内容决定的,封闭的路径可能是“外轮廓”或“内轮廓(内孔)”,这主要由其方向(顺时针或者逆时针)决定的
多个路径可以添加进Paths结构体组成一组路径。
Paths
由多个Path组成的基本类型;
可以包含开轮廓或者闭合轮廓;
InitOptions
IntRect
用于接受Clipper库的GetBounds()函数的结果(包围盒);
ClipType
总共有四种裁剪运算类型:AND、OR、NOT和XOR
他们的类型主要取决于他们的点集信息和填充规则,规则如下:
AND(Intersection求交):获取两者相交的部分;
OR(Union求并):获取两者并集部分;
NOT(difference求异):获取Clip区域以外的区域;
XOR(exclusive求异或):获取两个区域互不重复的区域;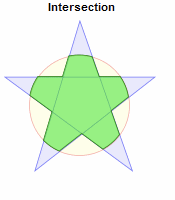

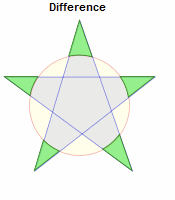
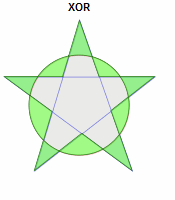
所有的多边形裁剪都是通过一个Clipper对象通过传递一个具体的布尔运算类型给它的Execute方法来实现的
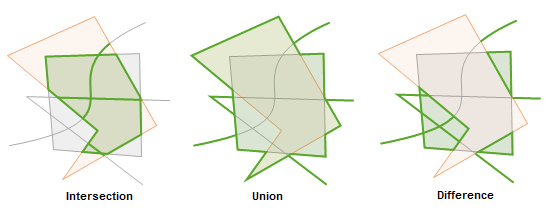
考虑到非封闭线段(多线段),裁剪的原则基本上和封闭图形是相同的。但是,如果一个裁剪案例中出现了以下几种基本情况,会采取以下裁剪原则:
并集:多线段将会被任何重叠的多边形裁剪,导致没有被覆盖的部分会联通重叠多边形一起返回;
交集、非运算和异或运算:多线段只会被Clip的多边形切割,并且在多线段原多边形之间不会有任何交点;
PolyType
多边形的布尔运算类型主要来设置两组多边形的属性,来分别代表被裁剪(subject)和裁剪(clip)的多边形。无论何时路径组(Paths)被添加到Clipper对象中,它们都应该被指定类型到底是subject还是clip。
求和运算(UNION)可以在单个路径组或两个路径组当中,但是所有其他的布尔运算需要设定两个路径组的类型获取有意义的结果。
PolyFillType
FILLing(填充)代指存在一个封闭路径内的区域,Clipper主要支持4种情况:Even-Odd、Non-Zero、Positive以及Negative;
最简单的填充策略属于Even-Odd(有时候称为可选择性填充Alternate filling)。给定了一组封闭路径,从该组路径的外侧的一个点出发,通过一根假想的线,当第一个被交到的路径将会被填充,当下一个路径相交时,则不被填充。同样的,每次一个路径是被环绕的,都会交叠式的被填充;
和Even-Odd填充方式不同,其他填充准则都是基于“边缘方向”和“环绕次数”。轮廓的方向是由点集的顺序决定的,同时轮廓的方向也是用来决定环绕次数的依据。
环绕次数的获取方法:
1. 从0开始计数;
2. 从整个轮廓组外一点p1,直到需要确认填充与否的区域内一点p2;
3. 当遍历p1到p2的每一个经过的点时,对于每一个穿越了这条假想线段如果是由右向左穿越,则穿越数+1,如果是从左向右穿越,则-1;
4. 得到最终的穿越数,即环绕次数;

Even-Odd:计数次环绕的部分被填充,偶数次的部分不填充;
Non-Zero:所有的非零环绕次数部分都被填充;
Positive:所有环绕次数大于零的部分被填充;
Negative:所有环绕次数小于零的被填充;
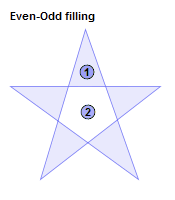
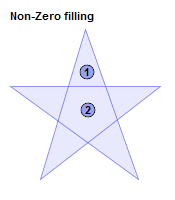

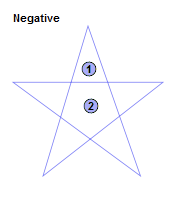
多边形是由一系列的自交或者不自交的封闭线段构成:一个单独多边形区域(单连通域)可以定义为一个无自交的路径,常常由一个外轮廓和多个内轮廓(可以没有内轮廓)构成。
目前最广泛使用的填充原则是:Even-Odd和Non-Zero
有一条定律是轮廓的方向不会影响最终计算出环绕次数奇偶性(这也是为什么在Even-Odd中方向性不需要确定的原因)
Y轴的方向的确会影响多边形的顺逆时针性。但是,改变Y轴的方向只会改变环绕次数的正负号,包括量级和各类填充方法的结果,是不会改变的。
JoinType
当在ClipperOffset对象中通过AddPaths函数添加路径时,相交类型参数可从jtMiter,jtSquare和jtRound中选一个;
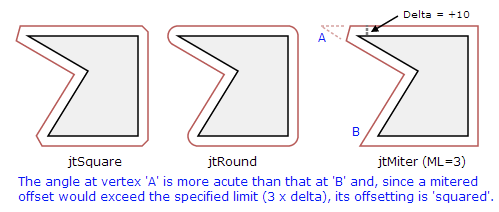
jtMiter:对于斜接式交点来说,有必要设定一个阀值,因为偏置的轮廓在极其窄的相交点处可能会造成“尖角”。为了将这些潜在的尖角包含在内,ClippperOffset对象的MiterLimit属性用来制定一个偏置点所能容忍的最大值;对于所有给定的边缘交点处,一旦斜接式交点超过了该阀值,那么方形交角将会被应用;
jtRound:当扁平的路径始终无法完美的获取角度信息,他们等价于一系列的圆弧曲线(可以查阅ClipperObject和ArcTolerance属性)
jtSquare:相当于斜接式当中的delta值始终为1的情况;
EndType
关于EndType(结束类型)总共有五种值:
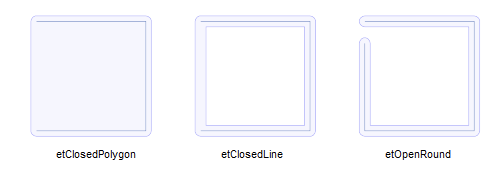
etClosedPolygon:末点是相交的,并且使用了JoinType来使路径视作一个多边形填充;
etClosedLine:末点是相交的,并且使用了JoinType来使路径视作一条线进行填充;
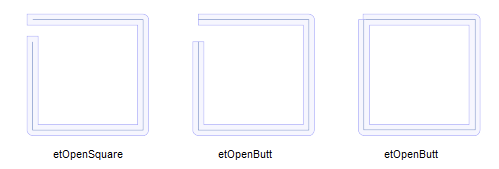
etOpenSqure:末点使用方形尾和扩展的delta角度;
etOpenRound:末点使用圆形尾和扩展的delta角度;
etOpenButt:末点使用了方向尾,没有任何扩展;
注意:在etClosedPolygon和etClosedLine类型中,无论首末点是否重合,路径结束的情况将会相同。(主要针对部分图形格式,规定首末点相同,这里Clipper统一采用了非首末点相同的情况)
ZFillFunction
类
ClipperBase
ClipperBase是Clipper的一个抽象基类,不应当直接单独实例话使用一个ClipperBase对象
ClipperBase.AddPath
任何数量的实体路径和剪切路径都可以被添加到一个AddPath()方法中去,或者通过AddPaths()来实现添加到一个组中去,或者两者混用;
实体路径可以是开线段集或者是闭合线段,但是裁剪线段必须是闭合的;
在闭合的路径中,*方向问题*应当结合filling rule来进行考虑,并且是通过Clipper库当中的Execute()方法来传递的;
路径的坐标范围:类似前中文的IntPoint范围;
返回值内容:如果输入的路径不正确,该函数会返回false;在以下情况路径会被视为不正确:
该路径少于两个点;
有两个点但是不是一个开放路径;
点集全部是共线的但是不是一个开放路径;
ClipperBase.AddPaths
同AddPath
ClipperBase.Clear
Clear()方法去除了Clipper对象中所有存在的被裁剪对象和裁剪对象,使得该Clipper对象可以重用
ClipperBase.GetBounds
该方法会返回Clipper对象中包含的所有多边形的最小包围矩形(该矩形长和高和坐标轴平行)。
Clipper
继承自*ClipperBase*
Clipper类将布尔运算内容(包含交并否异或)进行封装,称之为多边形裁剪;
输入的多边形,不管是subject还是clip,都通过AddPath或者AddPaths方法传递给Clipper对象,最后使用Execute函数进行裁剪,多个布尔运算可以通过输入相同的多边形,然后反复执行Execute函数来实现;
Clipper.Constructor
构建一个Clipper对象,可以使用InitOptions来进行初始化;
Clipper.Execute
一旦裁剪路径组和被裁剪路径组已经被设定(通过AddPath后者AddPaths方法),*Execute*方法可以执行布尔运算,具体运算类型由clipType来指定;
最终的solution参数可以是一个路径组(Path)或者一个多边形树(PolyTree)类型。因为路径结构比多边形树结构简单,所以效率相对较高(10%);但是,PolyTree的信息结构可能提供给了用户更多的有用信息。首先,PolyTree结构保留了网状的多边形父子关系(例如外轮廓包含孔洞,孔洞内包含内轮廓等)。相同的,只有PolyTree类型可以区别开轮廓和闭合轮廓,因为每一个PolyNode结构有IsOpen属性(Path类型没有任何成员来告知它是否为开放的还是闭合的),正因为如此,当一个开放轮廓组被传递给一个Clipper对象,使用者必须用一个PolyTree类型来接收solution的结果,否则会引起错误;
当在使用开放路径进行裁剪时,Clipper库提供了两个有效的函数来快速的分离结果当中的开放路径部分和闭合轮廓组部分OpenPathsFromPolyTree和ClosedPathsFromPolyTree。同时Clipper也提供了PolyTreeToPaths来快速将PolyTree类型转换为Paths。

关于solution返回的路径组,有以下几点需要注意:
并没有固定的顺序;
不会出现叠加和自交的情况;
内孔的方向永远和外孔相反;
solution的填充类型可以认为是Even-Odd或者Non-Zero中任意一种,即兼容这两种填充方式;
被填充图形填充类型(subjFillTYpe)和裁剪图形填充类型(clipFillType)决定了多边形的填充规则和相对规则;
Execute可以执行多次,不需要重置,即可以对一个多边形进行多次Execute的处理。
Clipper.PreserveCollinear
默认的,当输入被裁剪和裁剪多边形的内容中三个或者更多的点是共线的,Clipper对象会在进行布尔运算之前对多余的共线点进行删除;当设定PreserveColinear属性防止了这种行为,来允许共线的点的情况出现在结果当中;
Clipper.StrictlySimple
术语:
一个简单多边形是指没有自交现象的多边形;
一个弱简单的多边形是指一个简单多边形包含重合点以及重合的线段;
一个强简单多边形是指一个简单多边形不包含重合点以及重合的线段;
对于点“重合”的定义是指如果多边形内的两个以上的点具有相同的坐标(并在序列上来说不是相邻点,即相邻点除外)。一条边接触到另一条边的定义是指这条边的一个端点与接触到另一条边(相邻边除外)相接触,或者他们是共线或覆盖关系(包括相邻边)。
由Clipper库的裁剪操作返回的多边形都是简单多边形,当StrictlySimple属性被启用,返回的多边形将会是是强简单多边形,否则会返回弱简单多边形。算法因为计算强简单多边形太大,导致该选项是默认关闭的。
注意:目前无法保证输出多边形是严格简单的,因为“简单化”工作还在进行当中;
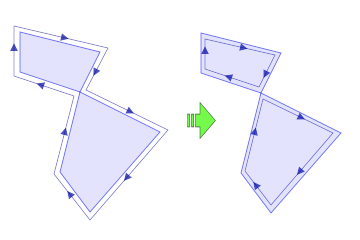

上面两张图显示出两个弱简单多边形被打断为强简单多边形(外围轮廓的方向是为了避免视觉上点集顺序的错误)
Clipper.ReverseSolution
当这个属性被设定为true时,由Execute方法返回的函数将会与其正常方向相反;
ClipperOffset
ClipperOffset.AddPath
向ClipperOffset对象添加一个路径用来准备偏置;
其中开放式路径只能被偏移一个正值;
CLipperOffset.AddPaths
同AddPath,添加路径
ClipperOffset.Constructor
构造函数包含了两个可选参数,MiterLimit和ArcTolerance,这两个参数和其同名的属性的含义是相同的。MiterLimit只是在JoinType是jtMiter的时候才启用,ArcTolerance只有在JoinType是jtRound或者当EndType是开放式轮廓的时候才有效;
ClipperOffset.Execute
该方法有两个参数,第一个是接受结果的结构(可以是PolyTree或Paths中的一种),第二个参数是指偏移量的大小--*负值会缩水,正值会膨胀*
该方法可以被调用多次,来实现对相同路径实现不同程度的偏置

ClipperOffset.Clear
清空所有多边形对象
ClipperOffset.Arctolerance
ClipperOffset.MiterLimit
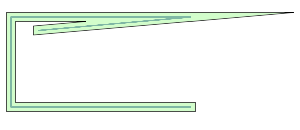
该属性包含了一个比例系数(=最大容忍距离/偏置距离),当大于最大容忍距离时,则会使用1*delta距离来进行;
*默认的MiterLimit值大小是2*,这也是允许的最小MiterLimit大小,如果没有规定合理的MiterLimit,在部分尖锐的拐角处就会形成长的突起,如下图:
PolyTree
*继承自PolyNode*
PolyTree被设计成一个*只读*数据结构,只能用来接收裁剪或者偏置的结果。一般在结果中经常会选择是否使用Paths或者PolyTree来获取最终的结果;PolyTree数据结构优于Paths,能够正确反应返回类型的*父子关系*,能够对开放路径和闭合轮廓进行区别。也正因为PolyTree有着比Paths更复杂的结构,导致算法效率下降大约5%以上,PolyTree目前只能用于寻找父子关系或开放路径需要考虑的场合;
在Clipper.Execute和ClipperOffset.Execute两个函数中,可以使用一个空的PolyTree对象来作为接收solution参数接收结果,一旦裁剪工作和偏置工作完成后,函数就会将结果已PolyTree的形式返回出来;
一个PolyTree对象可以包含任何数目的PolyNode子对象,其中每一个PolyNode代表了多边形的一个轮廓(内轮廓或者外轮廓)。PolyTree本身就是一个特殊的PolyNode对象,它的子对象即代表结果中了最高级别的外轮廓,而它自身的Contour数据始终为空,被包含的最高级别的PolyNode还可能包含它自己的子对象(内孔),甚至自己的内孔还可以包括被嵌套的外轮廓等。但是外轮廓的子对象永远是孔,孔的子对象永远是外轮廓。
PolyTree可以包含开放路径。开放路径永远会在最高级别的子轮廓中存储,提供了两个函数可以快速的分离提取PolyTree开放路径和封闭轮廓---OpenPathsFromPolyTree和ClosedPathsFromPolyTree。

PolyTree.GetFirst
该方法返回第一个有效的polygon的PolyNode的指针,否则返回空;
该方法等价于调用Child[0]除非一个PolyTree的对象为空(无任何子对象),这种情况下使用Child[0]会产生越界。
PolyTree.Total
返回该PolyTree所包含的所有PolyNodes的数量,该值不应和ChildCount混淆,后者是返回当前PolyNode所包含的下一层子轮廓数量。
PolyTree.Clear
该方法将删除PolyTree对象中所有的子对象。
Clear一般不需要显式调用,每次执行Clipper.Execute方法每次接受一个PolyTree参数,并在生成新的结果之前会自动清楚其中的内容。同样的,PolyTree的析构函数会自动清理其内部包含的PolyNode。
PolyNode
PolyNodes是被封装在PolyTree的容器中,同时提供了一个数据结构来代表由Excute()方法返回的多边形轮廓中的父子关系。
一个PolyNode对象代表一个多边形;它的“IsHole”属性表明它是一个“外轮廓”还是一个“内孔”,PolyNodes可能包含任意数量的PolyNode子对象,一般为外轮廓的子对象是内轮廓,而内轮廓的子对象是(嵌套的)外轮廓;
PolyNode.ChildCount
返回一个PolyNode所有子对象数量
PolyNode.Contour
返回该路径的一系列(List)点集坐标;
PolyNode.GetNext
该方法返回的PolyNode将会是第一个子对象,然后依次是下一个对象,否则是下一个对象;
一个PolyTree可以很方便的被遍历,通过使用GetFIrst(),然后接下来使用GetNext()知道最终返回一个空指针;
PolyNode.IsHole
当该PolyNode为孔洞时,返回True;
外轮廓的子对象永远是孔洞,同时孔洞的子对象永远是(被嵌套)外轮廓;
对于PolyNode来说没有定义IsHole属性,但是其最高层的子对象永远都是外轮廓;
PolyNode.IsOpen
当该轮廓为开放路径时该属性为True,只有最高级的PolyNode才可以包含开放轮廓;
PolyNode.Parent
返回父节点;
对于PolyTree对象(同样是一个PolyNode)来说没有父对象,将会返回一个空指针;
函数
Area
该函数返回多边形的面积(默认输入的多边形为封闭轮廓)。根据方向的不同,该值大小可能为正或负。如果方向为正,则结果为正;如果方向为负,则结果为负;
CleanPolygon
主要用来移除以下类型的点集:
连接点共线的边,或者近似共线的边(那么在指定距离内不会存在共线点);
距离过近的相邻点(在指定范围内);
在次相邻的线段以及无关线段之间距离过小(在指定范围之内);
次相邻是指两个点之间还有一个点(无关点);
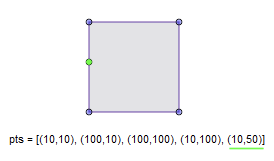
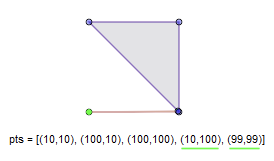
函数中的distance默认值为√2,所有轮廓上每个点如果在X或者Y方向上与相邻点或者次相邻点之间的距离小于1个单位的点将会被去除。(如果相邻边无关点次相邻也会被移除)
C++限定:该函数被重载,在第一种定义中,in_poly和out_poly可以指同一个路径,来防止进入到第二种重载就自动清楚Path中的内容(第二种指Paths)
CleanPolygons
和CleanPolgon相同
ClosedPathsFromPolyTree
从PolyTree中提取闭合轮廓部分
OpenPathsFromPolyTree
从PolyTree中提取开放路径部分
MinkowskiDiff
闵可夫斯基差,用来检测多边形碰撞使用
MinkowskiSum
闵可夫斯基和
Orientation
方向只有在封闭的曲线里面是重要的,方向的定义就是在给定的封闭曲线中给出点集是按照顺时针还是逆时针进行排列;
方向同样和轴的方向有关联:
在Y轴向上显示的模式中,方向变量为true对应的是逆时针轮廓;
在Y轴向下显示模式中,方向变量为true对应的是顺时针轮廓;
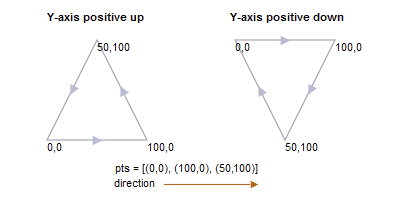
*注意*
自交多边形有着不确定的方向性,此时函数不会返回一个有意义的值;
大部分2D图形显示库(例如GDI、GDI+)甚至SVG文件格式有其坐标原点(在左上角,Y轴向下)。但是,一部分显示库(OpenGL等),可以自定义坐标原点,或者自定义Y方向朝上;
对于Non-Zero填充的多边形,内环(内孔) 的方向必须与外环相反;
对于由Clipper库的Execute方法,他们的外孔结果永远为true,内孔结果永远为false;(除非ReverseSolution属性已经被启用)
PointInPolygon
判断点是否在多边形内,如果返回0则是不在,-1则在多边形边缘上,1在多边形内;
PolyTreeToPaths
将PolyTree类型数据转换为Paths数据
ReversePath
将点集组进行倒序排列
ReversePaths
将点集组进行倒序排列
SimplifyPolygon
将自交部分从自身的部分剔除(通过指定一个FillType来实现一个布尔求和操作)
多个没有相邻重复点(或者说没有"接触")的多边形将会被分割为两个多边形组;
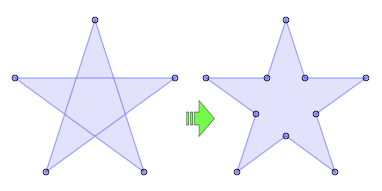
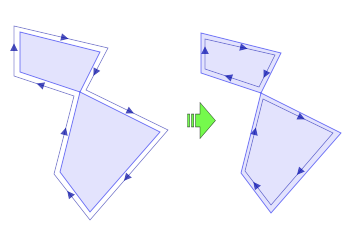

SimplifyPolygons
同SimplifyPolygon
转自:https://www.cnblogs.com/zhigu/p/11943118.html