C# UTM坐标和WGS84坐标转换小工具

工具根据：http://home.hiwaay.net/~taylorc/toolbox/geography/geoutm.html js代码改编

工具源码github:https://github.com/JeroLong/TUMAndWGS84TransTool.git

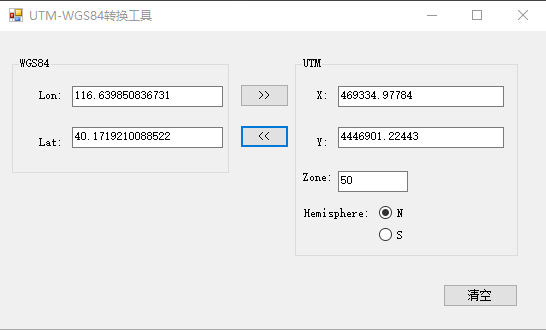
效果：

主要代码：

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace UTMAndWGS84TransTool
{
    public class UTMAndWGS84
    {
        static double pi = Math.PI;

        /* Ellipsoid model constants (actual values here are for WGS84) */
        static double sm_a = 6378137.0;
        static double sm_b = 6356752.314;
        static double sm_EccSquared = 6.69437999013e-03;

        static double UTMScaleFactor = 0.9996;


        /*
        * DegToRad
        *
        * Converts degrees to radians.
        *
        */
        private static double DegToRad(double deg)
        {
            return (deg / 180.0 * pi);
        }




        /*
        * RadToDeg
        *
        * Converts radians to degrees.
        *
        */
        private static double RadToDeg(double rad)
        {
            return (rad / pi * 180.0);
        }




        /*
        * ArcLengthOfMeridian
        *
        * Computes the ellipsoidal distance from the equator to a point at a
        * given latitude.
        *
        * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
        * GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
        *
        * Inputs:
        *     phi - Latitude of the point, in radians.
        *
        * Globals:
        *     sm_a - Ellipsoid model major axis.
        *     sm_b - Ellipsoid model minor axis.
        *
        * Returns:
        *     The ellipsoidal distance of the point from the equator, in meters.
        *
        */
        private static double ArcLengthOfMeridian(double phi)
        {
            double alpha, beta, gamma, delta, epsilon, n;
            double result;

            /* Precalculate n */
            n = (sm_a - sm_b) / (sm_a + sm_b);

            /* Precalculate alpha */
            alpha = ((sm_a + sm_b) / 2.0)
               * (1.0 + (Math.Pow(n, 2.0) / 4.0) + (Math.Pow(n, 4.0) / 64.0));

            /* Precalculate beta */
            beta = (-3.0 * n / 2.0) + (9.0 * Math.Pow(n, 3.0) / 16.0)
               + (-3.0 * Math.Pow(n, 5.0) / 32.0);

            /* Precalculate gamma */
            gamma = (15.0 * Math.Pow(n, 2.0) / 16.0)
                + (-15.0 * Math.Pow(n, 4.0) / 32.0);

            /* Precalculate delta */
            delta = (-35.0 * Math.Pow(n, 3.0) / 48.0)
                + (105.0 * Math.Pow(n, 5.0) / 256.0);

            /* Precalculate epsilon */
            epsilon = (315.0 * Math.Pow(n, 4.0) / 512.0);

            /* Now calculate the sum of the series and return */
            result = alpha
                * (phi + (beta * Math.Sin(2.0 * phi))
                    + (gamma * Math.Sin(4.0 * phi))
                    + (delta * Math.Sin(6.0 * phi))
                    + (epsilon * Math.Sin(8.0 * phi)));

            return result;
        }



        /*
        * UTMCentralMeridian
        *
        * Determines the central meridian for the given UTM zone.
        *
        * Inputs:
        *     zone - An integer value designating the UTM zone, range [1,60].
        *
        * Returns:
        *   The central meridian for the given UTM zone, in radians, or zero
        *   if the UTM zone parameter is outside the range [1,60].
        *   Range of the central meridian is the radian equivalent of [-177,+177].
        *
        */
        private static double UTMCentralMeridian(double zone)
        {
            double cmeridian;

            cmeridian = DegToRad(-183.0 + (zone * 6.0));

            return cmeridian;
        }



        /*
        * FootpointLatitude
        *
        * Computes the footpoint latitude for use in converting transverse
        * Mercator coordinates to ellipsoidal coordinates.
        *
        * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
        *   GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
        *
        * Inputs:
        *   y - The UTM northing coordinate, in meters.
        *
        * Returns:
        *   The footpoint latitude, in radians.
        *
        */
        private static double FootpointLatitude(double y)
        {
            double y_, alpha_, beta_, gamma_, delta_, epsilon_, n;
            double result;

            /* Precalculate n (Eq. 10.18) */
            n = (sm_a - sm_b) / (sm_a + sm_b);

            /* Precalculate alpha_ (Eq. 10.22) */
            /* (Same as alpha in Eq. 10.17) */
            alpha_ = ((sm_a + sm_b) / 2.0)
                * (1 + (Math.Pow(n, 2.0) / 4) + (Math.Pow(n, 4.0) / 64));

            /* Precalculate y_ (Eq. 10.23) */
            y_ = y / alpha_;

            /* Precalculate beta_ (Eq. 10.22) */
            beta_ = (3.0 * n / 2.0) + (-27.0 * Math.Pow(n, 3.0) / 32.0)
                + (269.0 * Math.Pow(n, 5.0) / 512.0);

            /* Precalculate gamma_ (Eq. 10.22) */
            gamma_ = (21.0 * Math.Pow(n, 2.0) / 16.0)
                + (-55.0 * Math.Pow(n, 4.0) / 32.0);

            /* Precalculate delta_ (Eq. 10.22) */
            delta_ = (151.0 * Math.Pow(n, 3.0) / 96.0)
                + (-417.0 * Math.Pow(n, 5.0) / 128.0);

            /* Precalculate epsilon_ (Eq. 10.22) */
            epsilon_ = (1097.0 * Math.Pow(n, 4.0) / 512.0);

            /* Now calculate the sum of the series (Eq. 10.21) */
            result = y_ + (beta_ * Math.Sin(2.0 * y_))
                + (gamma_ * Math.Sin(4.0 * y_))
                + (delta_ * Math.Sin(6.0 * y_))
                + (epsilon_ * Math.Sin(8.0 * y_));

            return result;
        }



        /*
        * MapLatLonToXY
        *
        * Converts a latitude/longitude pair to x and y coordinates in the
        * Transverse Mercator projection.  Note that Transverse Mercator is not
        * the same as UTM; a scale factor is required to convert between them.
        *
        * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
        * GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
        *
        * Inputs:
        *    phi - Latitude of the point, in radians.
        *    lambda - Longitude of the point, in radians.
        *    lambda0 - Longitude of the central meridian to be used, in radians.
        *
        * Outputs:
        *    xy - A 2-element array containing the x and y coordinates
        *         of the computed point.
        *
        * Returns:
        *    The function does not return a value.
        *
        */
        private static void MapLatLonToXY(double phi, double lambda, double lambda0, out double[] xy)
        {
            double N, nu2, ep2, t, t2, l;
            double l3coef, l4coef, l5coef, l6coef, l7coef, l8coef;
            double tmp;

            /* Precalculate ep2 */
            ep2 = (Math.Pow(sm_a, 2.0) - Math.Pow(sm_b, 2.0)) / Math.Pow(sm_b, 2.0);

            /* Precalculate nu2 */
            nu2 = ep2 * Math.Pow(Math.Cos(phi), 2.0);

            /* Precalculate N */
            N = Math.Pow(sm_a, 2.0) / (sm_b * Math.Sqrt(1 + nu2));

            /* Precalculate t */
            t = Math.Tan(phi);
            t2 = t * t;
            tmp = (t2 * t2 * t2) - Math.Pow(t, 6.0);

            /* Precalculate l */
            l = lambda - lambda0;

            /* Precalculate coefficients for l**n in the equations below
               so a normal human being can read the expressions for easting
               and northing
               -- l**1 and l**2 have coefficients of 1.0 */
            l3coef = 1.0 - t2 + nu2;

            l4coef = 5.0 - t2 + 9 * nu2 + 4.0 * (nu2 * nu2);

            l5coef = 5.0 - 18.0 * t2 + (t2 * t2) + 14.0 * nu2
                - 58.0 * t2 * nu2;

            l6coef = 61.0 - 58.0 * t2 + (t2 * t2) + 270.0 * nu2
                - 330.0 * t2 * nu2;

            l7coef = 61.0 - 479.0 * t2 + 179.0 * (t2 * t2) - (t2 * t2 * t2);

            l8coef = 1385.0 - 3111.0 * t2 + 543.0 * (t2 * t2) - (t2 * t2 * t2);

            xy = new double[2];
            /* Calculate easting (x) */
            xy[0] = N * Math.Cos(phi) * l
                + (N / 6.0 * Math.Pow(Math.Cos(phi), 3.0) * l3coef * Math.Pow(l, 3.0))
                + (N / 120.0 * Math.Pow(Math.Cos(phi), 5.0) * l5coef * Math.Pow(l, 5.0))
                + (N / 5040.0 * Math.Pow(Math.Cos(phi), 7.0) * l7coef * Math.Pow(l, 7.0));

            /* Calculate northing (y) */
            xy[1] = ArcLengthOfMeridian(phi)
                + (t / 2.0 * N * Math.Pow(Math.Cos(phi), 2.0) * Math.Pow(l, 2.0))
                + (t / 24.0 * N * Math.Pow(Math.Cos(phi), 4.0) * l4coef * Math.Pow(l, 4.0))
                + (t / 720.0 * N * Math.Pow(Math.Cos(phi), 6.0) * l6coef * Math.Pow(l, 6.0))
                + (t / 40320.0 * N * Math.Pow(Math.Cos(phi), 8.0) * l8coef * Math.Pow(l, 8.0));

            return;
        }



        /*
        * MapXYToLatLon
        *
        * Converts x and y coordinates in the Transverse Mercator projection to
        * a latitude/longitude pair.  Note that Transverse Mercator is not
        * the same as UTM; a scale factor is required to convert between them.
        *
        * Reference: Hoffmann-Wellenhof, B., Lichtenegger, H., and Collins, J.,
        *   GPS: Theory and Practice, 3rd ed.  New York: Springer-Verlag Wien, 1994.
        *
        * Inputs:
        *   x - The easting of the point, in meters.
        *   y - The northing of the point, in meters.
        *   lambda0 - Longitude of the central meridian to be used, in radians.
        *
        * Outputs:
        *   philambda - A 2-element containing the latitude and longitude
        *               in radians.
        *
        * Returns:
        *   The function does not return a value.
        *
        * Remarks:
        *   The local variables Nf, nuf2, tf, and tf2 serve the same purpose as
        *   N, nu2, t, and t2 in MapLatLonToXY, but they are computed with respect
        *   to the footpoint latitude phif.
        *
        *   x1frac, x2frac, x2poly, x3poly, etc. are to enhance readability and
        *   to optimize computations.
        *
        */
        private static void MapXYToLatLon(double x, double y, double lambda0, out double[] xy)
        {
            double phif, Nf, Nfpow, nuf2, ep2, tf, tf2, tf4, cf;
            double x1frac, x2frac, x3frac, x4frac, x5frac, x6frac, x7frac, x8frac;
            double x2poly, x3poly, x4poly, x5poly, x6poly, x7poly, x8poly;

            /* Get the value of phif, the footpoint latitude. */
            phif = FootpointLatitude(y);

            /* Precalculate ep2 */
            ep2 = (Math.Pow(sm_a, 2.0) - Math.Pow(sm_b, 2.0))
                  / Math.Pow(sm_b, 2.0);

            /* Precalculate cos (phif) */
            cf = Math.Cos(phif);

            /* Precalculate nuf2 */
            nuf2 = ep2 * Math.Pow(cf, 2.0);

            /* Precalculate Nf and initialize Nfpow */
            Nf = Math.Pow(sm_a, 2.0) / (sm_b * Math.Sqrt(1 + nuf2));
            Nfpow = Nf;

            /* Precalculate tf */
            tf = Math.Tan(phif);
            tf2 = tf * tf;
            tf4 = tf2 * tf2;

            /* Precalculate fractional coefficients for x**n in the equations
               below to simplify the expressions for latitude and longitude. */
            x1frac = 1.0 / (Nfpow * cf);

            Nfpow *= Nf;   /* now equals Nf**2) */
            x2frac = tf / (2.0 * Nfpow);

            Nfpow *= Nf;   /* now equals Nf**3) */
            x3frac = 1.0 / (6.0 * Nfpow * cf);

            Nfpow *= Nf;   /* now equals Nf**4) */
            x4frac = tf / (24.0 * Nfpow);

            Nfpow *= Nf;   /* now equals Nf**5) */
            x5frac = 1.0 / (120.0 * Nfpow * cf);

            Nfpow *= Nf;   /* now equals Nf**6) */
            x6frac = tf / (720.0 * Nfpow);

            Nfpow *= Nf;   /* now equals Nf**7) */
            x7frac = 1.0 / (5040.0 * Nfpow * cf);

            Nfpow *= Nf;   /* now equals Nf**8) */
            x8frac = tf / (40320.0 * Nfpow);

            /* Precalculate polynomial coefficients for x**n.
               -- x**1 does not have a polynomial coefficient. */
            x2poly = -1.0 - nuf2;

            x3poly = -1.0 - 2 * tf2 - nuf2;

            x4poly = 5.0 + 3.0 * tf2 + 6.0 * nuf2 - 6.0 * tf2 * nuf2
                - 3.0 * (nuf2 * nuf2) - 9.0 * tf2 * (nuf2 * nuf2);

            x5poly = 5.0 + 28.0 * tf2 + 24.0 * tf4 + 6.0 * nuf2 + 8.0 * tf2 * nuf2;

            x6poly = -61.0 - 90.0 * tf2 - 45.0 * tf4 - 107.0 * nuf2
                + 162.0 * tf2 * nuf2;

            x7poly = -61.0 - 662.0 * tf2 - 1320.0 * tf4 - 720.0 * (tf4 * tf2);

            x8poly = 1385.0 + 3633.0 * tf2 + 4095.0 * tf4 + 1575 * (tf4 * tf2);
            xy = new double[2];
            /* Calculate latitude */
            xy[0] = phif + x2frac * x2poly * (x * x)
                + x4frac * x4poly * Math.Pow(x, 4.0)
                + x6frac * x6poly * Math.Pow(x, 6.0)
                + x8frac * x8poly * Math.Pow(x, 8.0);

            /* Calculate longitude */
            xy[1] = lambda0 + x1frac * x
                + x3frac * x3poly * Math.Pow(x, 3.0)
                + x5frac * x5poly * Math.Pow(x, 5.0)
                + x7frac * x7poly * Math.Pow(x, 7.0);

            return;
        }




        /*
        * LatLonToUTMXY
        *
        * Converts a latitude/longitude pair to x and y coordinates in the
        * Universal Transverse Mercator projection.
        *
        * Inputs:
        *   lat - Latitude of the point, in radians.
        *   lon - Longitude of the point, in radians.
        *   zone - UTM zone to be used for calculating values for x and y.
        *          If zone is less than 1 or greater than 60, the routine
        *          will determine the appropriate zone from the value of lon.
        *
        * Outputs:
        *   xy - A 2-element array where the UTM x and y values will be stored.
        *
        * Returns:
        *   The UTM zone used for calculating the values of x and y.
        *
        */
        public static double[] LatLonToUTMXY(double lat, double lon)
        {
            double zone = Math.Floor((lon + 180.0) / 6) + 1;
            double[] xy = new double[2];
            MapLatLonToXY(DegToRad(lat),DegToRad (lon), UTMCentralMeridian(zone), out xy);

            /* Adjust easting and northing for UTM system. */
            xy[0] = xy[0] * UTMScaleFactor + 500000.0;
            xy[1] = xy[1] * UTMScaleFactor;
            if (xy[1] < 0.0)
                xy[1] = xy[1] + 10000000.0;

            return new double[] { xy[0], xy[1], zone };
        }



        /*
        * UTMXYToLatLon
        *
        * Converts x and y coordinates in the Universal Transverse Mercator
        * projection to a latitude/longitude pair.
        *
        * Inputs:
        *    x - The easting of the point, in meters.
        *    y - The northing of the point, in meters.
        *    zone - The UTM zone in which the point lies.
        *    southhemi - True if the point is in the southern hemisphere;
        *               false otherwise.
        *
        * Outputs:
        *    latlon - A 2-element array containing the latitude and
        *            longitude of the point, in radians.
        *
        * Returns:
        *    The function does not return a value.
        *
        */
        public static double[] UTMXYToLatLon(double x, double y, double zone, bool southhemi)
        {
            double cmeridian;

            x -= 500000.0;
            x /= UTMScaleFactor;

            /* If in southern hemisphere, adjust y accordingly. */
            if (southhemi)
                y -= 10000000.0;

            y /= UTMScaleFactor;

            cmeridian = UTMCentralMeridian(zone);
            double[] xy = new double[2];
            MapXYToLatLon(x, y, cmeridian, out xy);
            xy[0] = RadToDeg(xy[0]);
            xy[1] = RadToDeg(xy[1]);
            return xy;
        }
    }
}