1.背景
经常都在说http、https,都知道https是安全的,
但是,
为什么说http不安全呢?
为什么又说https是安全的呢?
接下来我将使用通俗易懂的方式给大家分析一下.......
2.深入解析
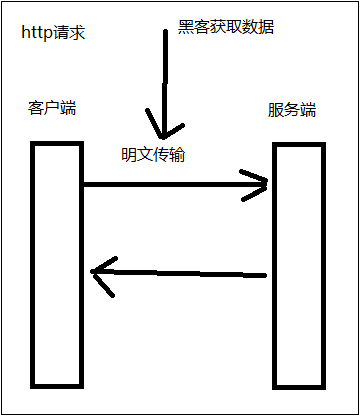
2.1.首先我们来看一下http请求
从下图可以看出,采用明文传输黑客可以直接获取。
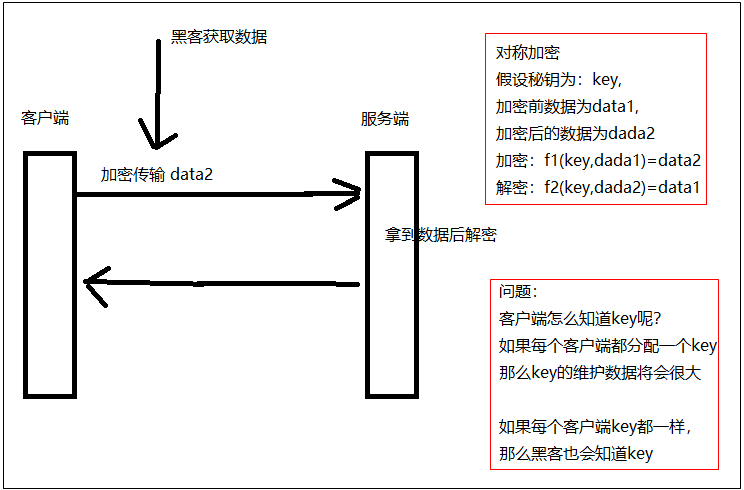
2.2.采用对称加密
表面上看采用对称加密后,就算黑客截取到数据没有key,也不知道数据内容
但问题是客户端怎么知道key呢?
如果给每个客户端都分配一个key,那么服务端要维护key与客户端的关系,这那么多客户端,这个数据维护将会很困难。
如果每个客户key一样,那么黑客也会知道key,加密就没有意义了。
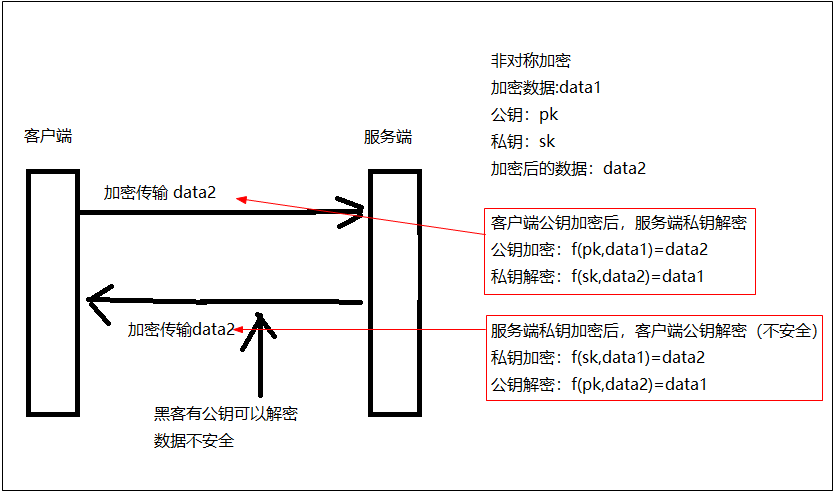
2.3.采用非对称加密
从下图可知,采用非对称加密的问题在于服务端在给客户端发送数据时,黑客有公钥可以解密数据导致不安全。
2.4.对称加密+非对称加密
1.客户端第一次请求的时候采用公钥加密,将key传到服务端,因为公钥加密的数据只有私钥才可以解密,所以是安全的的;
2.服务端接收到加密数据后,使用私钥解密,得到key;
3.在后面的请求中服务端客户端采用对称加密,key为加密码;
如下图:
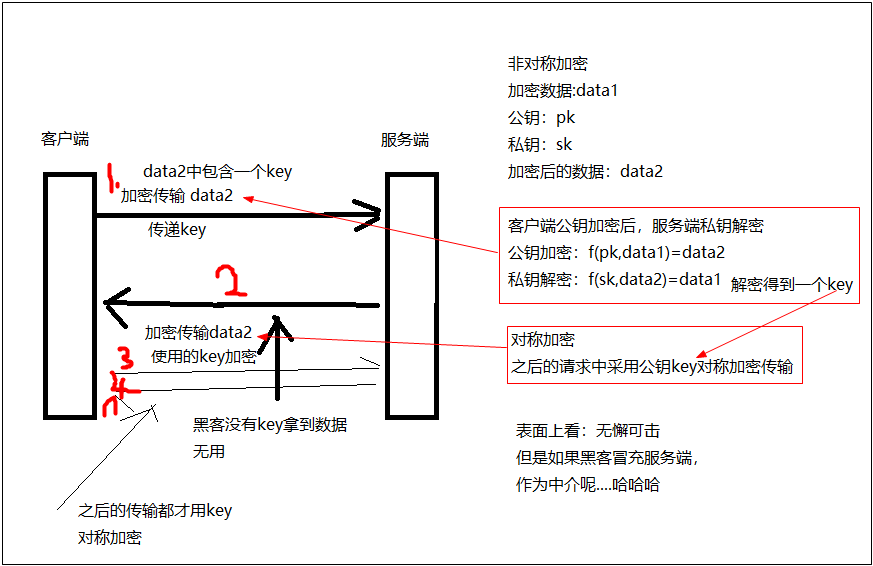
表面上看无懈可击,因为只有客户端自己与服务端知道加密的key,是安全的的,
但是,大家有没有想过客户端在获取公钥时,如果黑客冒充服务端给了一个假的公钥给客户端
客户端使用假的公钥加密数据有发给黑客的服务端,这时候黑客有与假公钥配对的私钥,
那么黑客就可以解密客户端发送的信息,进而黑客用真的公钥加密数据发送给服务端,在中间起到一个信息转发的作用
这样一来,所有的信息黑客都知道了,并且可篡改........太不安全了....
如下图所示:
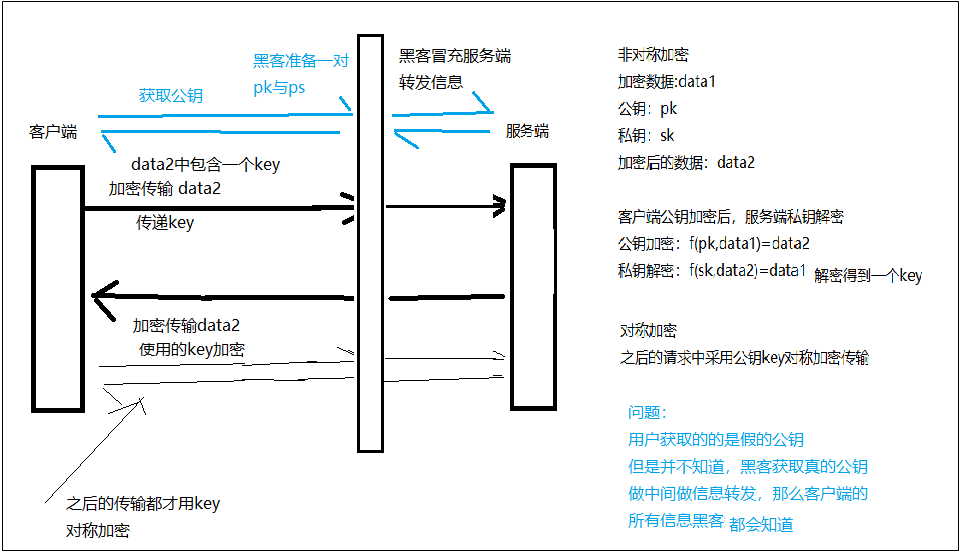
这里不安全的原因在于,获取到了黑客假的公钥,如果能保证公钥的真实性,那么这个方案就完美了
2.5.非对称加密+对称加密+CA证书
1.非对称加密+对称加密的方式不安全的根本原因是不能保证公钥的真实性
2.那么就产生的CA权威中心的概念,CA的角色就有点像,你说你是研究生毕业,别人不信呀,那怎么办,你的找一个权威机构(学校)颁发的证书别人才信
3.服务端就可以在CA权威中心申请一个证书,包括公钥pk2和私钥sk2
4.用户(客户端)的电脑上安装CA权威机构证书
基础的数据搞定后,接下来在分析一下请求流程
1.客户端向服务端发出请求获取公钥pk
2.服务端对公钥加密后返回给客户端pkdata,加密方式为:f(sk2,pk)=pkdata,这个pkdata只能是CA权威中心的公钥pk2才可以解密,得到服务端的公钥pk
3.客户端解密出公钥pk,解密方式为:f(pk2,pkdata)=pk,要解密这个客户端必须要有pk2,
那么这个pk2,从哪里来呢?CA权威中心通过网络获取,不行,这样会被黑客冒充
只能直接在客户端本地取,即:事先安装好证书,大家也可以查看直接电脑上已经安装好的证书,查看链接:https://jingyan.baidu.com/article/ff42efa9449a97c19f220250.html
4.非对称加密传递key到服务端,有了服务端的真实公钥pk后,用户就可以用公钥加密key发送到服务端;
5.服务端使用私钥解密获取到key;
6.之后的请服务端与客户端都采用key,进行对称加密传递数据;
黑客永远木有办法了...除非CA有内鬼......哈哈哈
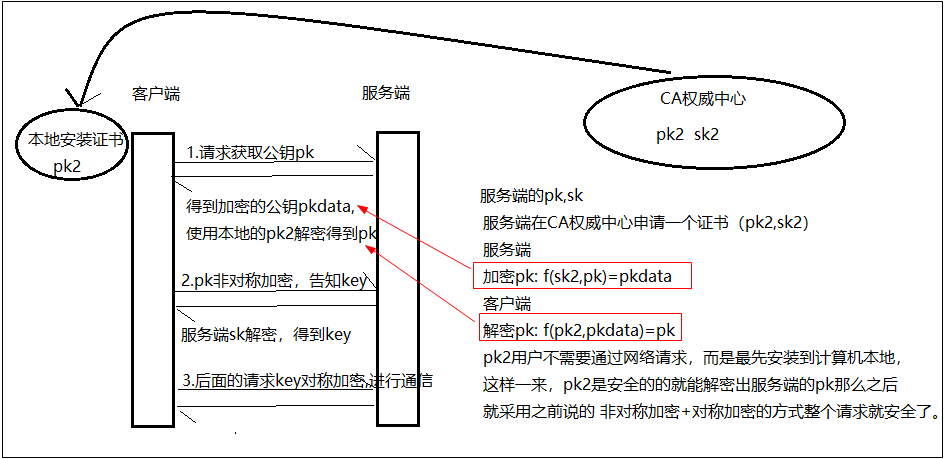
完美!