[ZJOI2015]幻想乡战略游戏

先考虑无修要怎么操作。

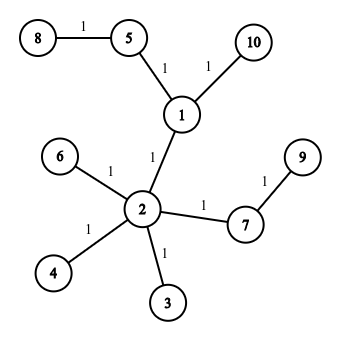
发现在无修的情况下，我们可以用一个换根(dp)解决。

那么带修改的情况要怎么办呢？

每次修改重新(dp)一遍不就行了（雾。

好的，让我们先来敲一个(O(N^2))的(dp)。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline ll ty() {
  char ch = getchar(); ll x = 0, f = 1;
  while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
  while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
  return x * f;
}

const int _ = 1e5 + 10;
const ll INF = 1e18;
int tot, head[_], to[_ << 1], nxt[_ << 1], edge[_ << 1];

void adde(int x, int y, int z) {
  to[++tot] = y;
  edge[tot] = z;
  nxt[tot] = head[x];
  head[x] = tot;
}

int N, M;
ll val[_], g[_], f[_], sum, ans;

void dfs(int x, int fa, ll d) {
  f[1] += d * val[x];
  g[x] = val[x];
  for (int i = head[x]; i; i = nxt[i]) {
    int y = to[i], z = edge[i];
    if (y == fa) continue;
    dfs(y, x, d + z);
    g[x] += g[y];
  }
}

void dp(int x, int fa) {
  ans = min(ans, f[x]);
  for (int i = head[x]; i; i = nxt[i]) {
    int y = to[i], z = edge[i];
    if (y == fa) continue;
    f[y] = f[x] - g[y] * z + (sum - g[y]) * z;
    dp(y, x);
  }
}

void work() {
  f[1] = 0, ans = INF;
  dfs(1, 0, 0);  //先以1为根，求出答案，然后进行换根dp
  dp(1, 0);
  printf("%lld
", ans);
}

int main() {
#ifndef ONLINE_JUDGE
  freopen("fantasy.in", "r", stdin);
  freopen("fantasy.out", "w", stdout);
#endif
  N = ty(), M = ty();
  for (int i = 1; i < N; ++i) {
    int x = ty(), y = ty(), z = ty();
    adde(x, y, z);
    adde(y, x, z);
  }
  while (M--) {
    int x = ty(), y = ty();
    val[x] += y, sum += y;
    work();  // 每修改一次，就重新dp一次2333
  }
  return 0;
}

然后就是这样的盛况：

“没事，卡卡常就过了。”@mzx

因为我太菜了，所以并没有把(O(N^2))卡常卡成(O(N log N))的能力。

先考虑一下这个(dp)的本质是什么，考虑从一个点(x)移动到点(y)，那么花费值的变化亮就是

[dis_{x,y} imes (sum - 2 imes g_y) ]

所以我们发现，当(sum-2 imes g_y)为负数的时候，答案便会减小，且可以证明每次这样的点唯一，所以实际上，我们可以从(root)开始出发，每次往(sum - 2 imes g_y)为负数的那个方向走，直到走不动时，就得到了最优解。

下面是动态点分治的内容了

发现主要是每次修改后，都需要从(root)节点重新开始寻找最优解，最坏情况下还是会达到(O(N^2))的复杂度，所以考虑如何优化这个过程。此时，就应该扯上点分树了。

假设我们能利用点分树求得答案，因为在点分树上只需要访问(log)个点，所以一次修改的复杂度就降到了(log)级别。

此时，正确的做法似乎逐渐浮出了水面：

假设当前所在的节点为(x)，那么我们枚举(x)在原树上的边，假设这条边的另一端为(y)，然后用(O(log N))的复杂度暴力计算出如果移动到(y)，花费是多少，如果花费减小，那么跳到点分树中对应的块上，然后再在对应的块里面求解，若不存在这样的边，那么肯定就是最优解。

现在思考一下这个做法需要维护哪些东西：

1. 每个块的点权和(sum_x)（点分树上(O(log N))修改）
2. (dist_x)：(x)在点分树上对应的联通块所有的点跳到(x)的花费
3. (sub_x)：(x)在点分树上对应的联通块所有的点跳到(x)在点分树上的父亲(fa_x)的花费

然后查询和修改不断暴跳父亲就好了。

#include <bits/stdc++.h>
using namespace std;

inline int ty() {
	char ch = getchar(); int x = 0, f = 1;
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}

typedef long long ll;
const int _ = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int N, M;
int tot, head[_], to[_ << 1], nxt[_ << 1], edge[_ << 1];

void adde(int x, int y, int z) {
	to[++tot] = y;
	edge[tot] = z;
	nxt[tot] = head[x];
	head[x] = tot;
}

namespace lca {
int fa[_], son[_], dep[_], dis[_], siz[_], top[_];
void dfs1(int x, int f) {
	siz[x] = 1;
	int maxx = 0;
	for (int i = head[x]; i; i = nxt[i]) {
		int y = to[i], z = edge[i];
		if (y == f) continue;
		fa[y] = x, dep[y] = dep[x] + 1, dis[y] = dis[x] + z;
		dfs1(y, x);
		siz[x] += siz[y];
		if (siz[y] > maxx) maxx = siz[y], son[x] = y;
	}
}
void dfs2(int x, int topf) {
	top[x] = topf;
	if (!son[x]) return;
	dfs2(son[x], topf);
	for (int i = head[x]; i; i = nxt[i]) {
		int y = to[i];
		if (y == fa[x] || y == son[x]) continue;
		dfs2(y, y);
	}
}
void init() {
	dep[1] = 1, dfs1(1, 0);
	dfs2(1, 1);
}
int query(int x, int y) {
	while (top[x] != top[y]) {
		if (dep[top[x]] < dep[top[y]]) swap(x, y);
		x = fa[top[x]];
	}
	return dep[x] < dep[y] ? x : y;
}
int dist(int x, int y) { return dis[x] + dis[y] - 2 * dis[query(x, y)]; }
} // namespace lca

int mxsiz, totsiz, root, siz[_], vis[_], fa[_];

void getroot(int x, int f) {
	siz[x] = 1;
	int maxx = 0;
	for (int i = head[x]; i; i = nxt[i]) {
		int y = to[i];
		if (vis[y] || y == f) continue;
		getroot(y, x);
		siz[x] += siz[y];
		maxx = max(maxx, siz[y]);
	}
	maxx = max(maxx, totsiz - siz[x]);
	if (maxx < mxsiz) mxsiz = maxx, root = x;
}

typedef pair<int, int> PII;
vector<PII> E[_];

void divide(int x) {
	vis[x] = true;
	int nowsiz = totsiz;
	for (int i = head[x]; i; i = nxt[i]) {
		int y = to[i];
		if (vis[y]) continue;
		mxsiz = INF, root = 0;
		totsiz = siz[y] > siz[x] ? nowsiz - siz[x] : siz[y];
		getroot(y, 0);
		E[x].push_back(make_pair(y, root));
		fa[root] = x;
		divide(root);
	}
}

ll sum[_];	// 点分树中以x为根的子树的权值和
ll dist[_];	// 点分树中以x为根的子树全部到x的花费
ll sub[_];	// 点分树中以x为根的子树全部到x在点分树上的父亲的花费

void modify(int x, int y) {
	sum[x] += y;
	for (int i = x; fa[i]; i = fa[i]) {
		int len = lca::dist(x, fa[i]);
		sum[fa[i]] += y;
		dist[fa[i]] += 1ll * y * len;
		sub[i] += 1ll * y * len;
	}
}

// 用一个log的代价直接计算以x为供应站时的花费
ll calc(int x) {
	ll ret = dist[x];
	for (int i = x; fa[i]; i = fa[i]) {
		int len = lca::dist(x, fa[i]);
		ret += 1ll * len * (sum[fa[i]] - sum[i]);
		ret += dist[fa[i]] - sub[i];
	}
	return ret;
}

ll query(int x) {
	// printf("%d
", x);
	ll cur = calc(x);
	for (auto p : E[x]) {
		int y = p.first, rt = p.second;
		// printf("%d %d
", y, rt);
		if (calc(y) < cur) return query(rt);
	}
	return cur;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("fantasy.in", "r", stdin);
	freopen("fantasy.out", "w", stdout);
#endif
	N = ty(), M = ty();
	for (int i = 1; i < N; ++i) {
		int x = ty(), y = ty(), z = ty();
		adde(x, y, z);
		adde(y, x, z);
	}
	lca::init();

	mxsiz = INF, totsiz = N, root = 0;
	getroot(1, 0);
	int RT = root;
	divide(root);

	while (M--) {
		// printf("!%d
", M);
		int x = ty(), y = ty();
		modify(x, y);
		printf("%lld
", query(RT));
	}
	return 0;
}