本文大部分内容来自于 hihoCoder,侵删。
本文只是将其用更好的格式进行展现,希望对读者有帮助。
定义
后缀自动机(( ext{Suffix Automaton}),简称 ( ext{SAM}))。对于一个字符串 (S),它对应的后缀自动机是一个最小的确定有限状态自动机(( ext{DFA})),接受且只接受 (S) 的后缀。
比如对于字符串 (S = underline{aabbabd}),它的后缀自动机是
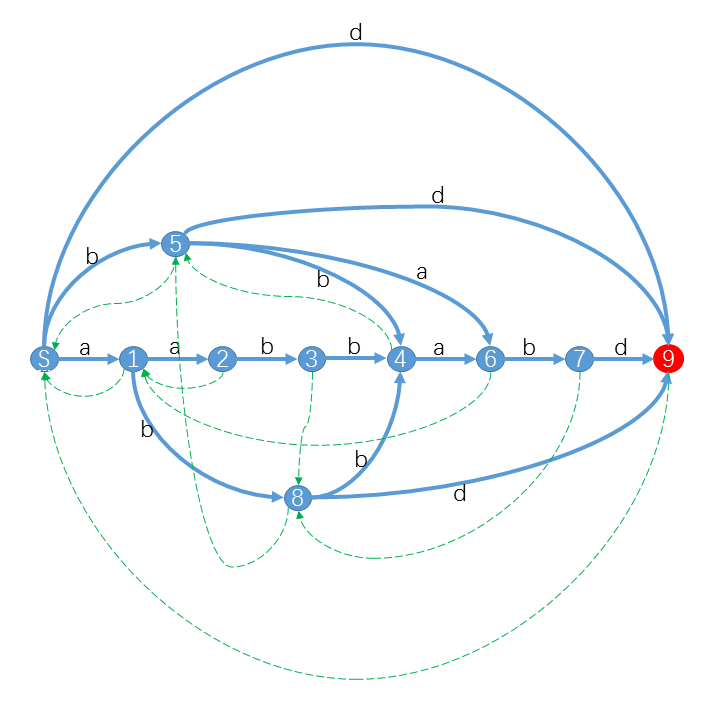
其中 红色状态 是终结状态。你可以发现对于 (S) 的后缀,我们都可以从 (S) 出发沿着字符标示的路径(蓝色实线)转移,最终到达终结状态。
特别的,对于 (S) 的子串,最终会到达一个合法状态。而对于其他不是 (S) 子串的字符串,最终会“无路可走”。
( ext{SAM}) 本质上是一个 ( ext{DFA}),( ext{DFA}) 可以用一个五元组 <字符集,状态集,转移函数、起始状态、终结状态集>来表示。至于 绿色虚线 那些虽然不是 ( ext{DFA}) 的一部分,但却是 ( ext{SAM}) 的重要部分,有了这些链接 ( ext{SAM}) 是如虎添翼,这些后面将再细讲。
下面先介绍对于一个给定的字符串 (S) 如何确定它对应的 状态集 和 转移函数 。
SAM 的状态集 (States)
首先先介绍一个概念 子串的结束位置集合 (endpos)
对于 (S) 的一个子串 (s),(endpos(s) = s) 在 (S) 中所有出现的结束位置集合。
以字符串 (S = underline{aabbabd}) 为例
| 状态 | 子串 | (endpos) |
|---|---|---|
| (S) | (varnothing) | ({0,1,2,3,4,5,6}) |
| (1) | (a) | ({{1,2,5}}) |
| (2) | (aa) | ({2}) |
| (3) | (aab) | ({3}) |
| (4) | (aabb,abb,bb) | ({4}) |
| (5) | (b) | ({3,4,6}) |
| (6) | (aabba,abba,bba,ba) | ({5}) |
| (7) | (aabbab,abbab,bbab,bab) | ({6}) |
| (8) | (ab) | ({3,6}) |
| (9) | (aabbabd,abbabd,bbabd,babd,abd,bd,d) | ({7}) |
我们把 (S) 的所有子串的 (endpos) 都求出来。如果两个子串的 (endpos) 相等,就把这两个子串归为一类。最终这些 (endpos) 的等价类就构成了 ( ext{SAM}) 的状态集合。
性质
-
对于S的两个子串 (s1) 和 (s2),不妨设 (|s1| le |s2|),那么 (s1) 是 (s2) 的后缀当且仅当 (endpos(s1) supseteq endpos(s2)),(s1) 不是 (s2) 的后缀当且仅当 (endpos(s1) cap endpos(s2) = varnothing)。
首先证明 (s1) 是 (s2) 的后缀 (Rightarrow) (endpos(s1) supseteq endpos(s2))。
既然 (s1) 是 (s2) 后缀,所以每次 (s2) 出现时 (s1) 也必然伴随出现,所以有 (endpos(s1) supseteq endpos(s2))。
再证明 (endpos(s1) supseteq endpos(s2)) (Rightarrow) (s1) 是 (s2) 的后缀。
我们知道对于 (S) 的子串 (s2),(endpos(s2))不会是空集,所以 (endpos(s1) supseteq endpos(s2)) (Rightarrow) 存在结束位置 (x) 使得 (s1) 结束于 (x),并且 (s2) 也结束于 (x),又 (|s1| le |s2|),所以 (s1) 是 (s2) 的后缀。
综上可知,(s1) 是 (s2) 的后缀当且仅当 (endpos(s1) supseteq endpos(s2))。
而 (s1) 不是 (s2) 的后缀当且仅当 (endpos(s1) cap endpos(s2) = varnothing)是一个简单的推论,不再赘述。
-
我们用 (substrings(st)) 表示状态 (st) 中包含的所有子串的集合,(longest(st)) 表示 (st) 包含的最长的子串,(shortest(st)) 表示 (st) 包含的最短的子串。
例如对于状态 (7),(substring(7)={aabbab,abbab,bbab,bab}),(longest(7)=aabbab),(shortest(7)=bab)。
-
( ext{SAM}) 中的一个状态包含的子串都具有相同的 (endpos),它们都互为后缀。
例如上图中状态 (4),({bb,abb,aabb})。
-
对于一个状态 (st),以及任意 (s in substrings(st)),都有 (s) 是 (longest(st))的后缀。
因为 (endpos(s)=endpos(longest(st))),所以 (endpos(s) supseteq endpos(longest(st))),根据刚才证明的结论有 (s) 是 (longest(st)) 的后缀。
-
对于一个状态 (st),以及任意的 (longest(st)) 的后缀 (s),如果 (s) 的长度满足:(length(shortest(st)) le length(s) le length(longsest(st))),那么 (s in substrings(st))。
因为 (length(shortest(st)) le length(s) le length(longsest(st)))
所以 (endpos(shortest(st)) supseteq endpos(s) supseteq endpos(longest(st)))
又 (endpos(shortest(st)) = endpos(longest(st)))
所以 (endpos(shortest(st)) = endpos(s) = endpos(longest(st)))
所以 (s in substrings(st))。
也就是说,(substrings(st)) 包含的是 (longest(st)) 的一系列 连续 后缀。
SAM 的后缀链接 (Suffix Links)
前面我们讲到 (substrings(st)) 包含的是 (longest(st)) 的一系列 连续 后缀。这连续的后缀在某个地方会“断掉”。
比如状态 (7),包含的子串依次是 (aabbab,abbab,bbab,bab) 。按照连续的规律下一个子串应该是 ("ab"),但是 ("ab") 没在状态 (7) 里。
这是为什么呢?
(aabbab,abbab,bbab,bab) 的 (endpos) 都是 ({6}),下一个 ("ab") 当然也在结束位置6出现过,但是 ("ab") 还在结束位置 (3) 出现过,所以 ("ab") 比 (aabbab,abbab,bbab,bab) 出现次数更多,于是就被分配到一个新的状态中。
所以,当 (longest(st)) 的某个后缀 (s) 在新的位置出现时,就会“断掉”,(s) 会属于新的状态。
于是我们可以发现一条状态序列:(7 ightarrow 8 ightarrow 5 ightarrow S)。这个序列的意义是 (longest(7)) 即 (aabbab) 的后缀依次在状态 (7,8,5,S) 中。我们用 后缀链接 (( ext{Suffix Link})) 这一串状态链接起来,这条 ( ext{link}) 就是上图中的 绿色虚线。
( ext{Suffix Links})后面会有妙用,我们暂且按下不表。
SAM 的转移函数 (Transition Function)
对于一个状态 (st),我们首先找到从它开始下一个遇到的字符可能是哪些。我们将 (st) 遇到的下一个字符集合记作 (next(st)),有 (next(st) = {S[i+1] | i in endpos(st)})。
例如 (next(S)={S[1], S[2], S[3], S[4], S[5], S[6], S[7]}={a, b, d}),(next(8)={S[4], S[7]}={b, d})。
对于一个状态 (st) 来说和一个 (next(st)) 中的字符 (c),发现 (substrings(st)) 中的所有子串后面接上一个字符 (c) 之后,新的子串仍然都属于同一个状态。
例如状态 (4),(next(4)={a}),(aabb,abb,bb) 后面接上字符 (a) 得到 (aabba,abba,bba),这些子串都属于状态(6)。
所以对于一个状态 (st) 和一个字符 (c in next(st)),可以定义转移函数 (trans(st, c) = x | longest(st) + c in substrings(x))。
也就是说,在 (longest(st))(因为无论哪个子串都会得到相同的结果)后面接上一个字符 (c) 得到一个新的子串 (s),找到包含 (s) 的状态 (x),那么 (trans(st, c)) 就等于 (x)。
算法构造
构造方法
使用 增量构造 的方法可以在 (O(|S|)) 的时间和空间复杂度中构造出 ( ext{SAM}),也就是从初始状态开始,每次添加一个字符 (S[1], S[2], dots S[n]),依次构造可以识别 (S[1], S[1dots 2], S[1dots 3], ... S[1dots N]=S) 的 ( ext{SAM})。
首先,为了实现 (O(|S|)) 的构造,每个状态肯定不能保存太多数据,例如 (substring(st)) 肯定不能保存下来了。对于一个状态 (st),只保存以下数据:
| 数据 | 含义 |
|---|---|
| (maxlen[st]) | (st) 包含的最长子串的长度 |
| (minlen[st]) | (st) 包含的最短子串的长度 |
| (trans[st][1dots c]) | (st) 的转移函数,(c) 为字符集大小 |
| (slink[st]) | (st) 的后缀链接 ( ext{(Suffix Link)}) |
假设已经构造好了 (S[1dots i]) 的 ( ext{SAM}),此时需要添加字符 (S[i+1]),于是新增了 (i+1) 个后缀需要识别:(S[1dots i+1],S[2dots i+1],dots,S[i+1])。由于这些新增状态分别是从(S[1dots i],S[2dots i],dots,"") 通过字符 (S[i+1]) 转移过来的,所以我们还需要对这些状态添加相应的转移。
假设 (S[1dots i]) 对应的状态是 (u),等价于 (S[1dots i]in substrings(u))。根据前面的讨论我们知道 (S[1dots i], S[2dots i], S[3dots i], dots , S[i], "") 对应的状态集合恰好就是从 (u) 到初始状态 (S) 的由 ( ext{Suffix Link}) 连接起来路径上的所有状态,不妨称这条路径 (上所有状态集合) 是 ( ext{suffix-path}(u ightarrow S))。
显然至少 (S[1dots i+1]) 这个子串不能被以前的 ( ext{SAM}) 识别,所以至少需要添加一个状态 (z),(z) 至少包含(S[1dots i+1])这个子串。
-
首先考虑最简单的一种情况:对于 ( ext{suffix-path}(u ightarrow S)) 的任意状态 (v),都有 (trans[v][S[i+1]]=NULL)。这时我们只要令 (trans[v][S[i+1]]=z),并且令 (slink[st]=S) 即可。
例如已经得到 ("aa") 的 ( ext{SAM}),现在希望构造 ("aab") 的 ( ext{SAM})。
此时 (u=2,z=3),( ext{suffix-path}(u ightarrow S)) 是桔色状态组成的路径 (2-1-S)。并且这 (3) 个状态都没有对应字符 (b) 的转移。所以我们只要添加红色转移 (trans[2][b]=trans[1][b]=trans[S][b]=z) 即可。以及 (slink[3]=S)。
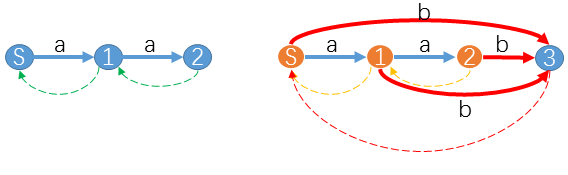
-
另一种复杂一点的情况是 ( ext{suffix-path}(u ightarrow S)) 上有一个节点 (v),使得 (trans[v][S[i+1]] eq NULL)。
先以下图为例。假设已经构造了 ("aabb") 的 ( ext{SAM}) 如图,现在我们要增加一个字符 (a) 构造 ("aabba") 的 ( ext{SAM})。
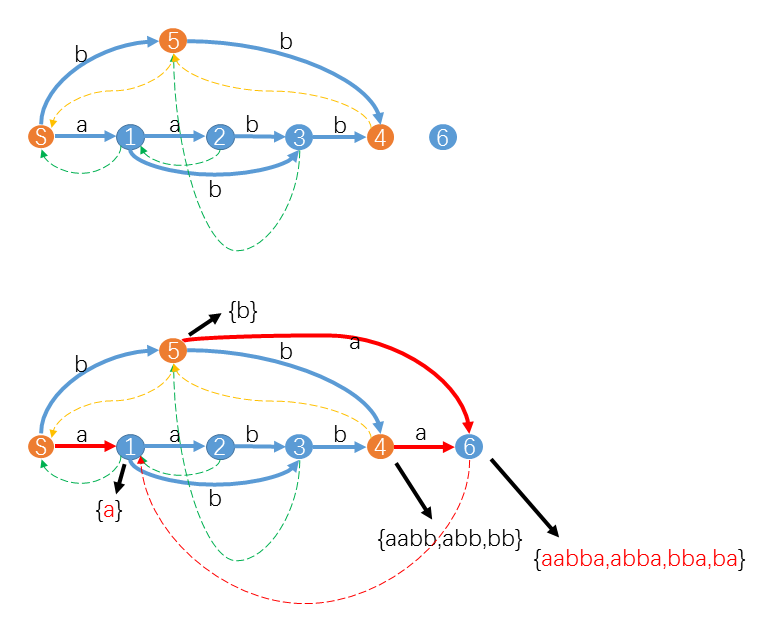
此时 (u=4,z=6),( ext{suffix-path}(u ightarrow S)) 是桔色状态组成的路径 (4-5-S)。对于状态 (4) 和状态 (5),由于它们都没有对应字符 (a) 的转移,所以我们只要添加红色转移 (trans[4][a]=trans[5][a]=z=6) 即可。但是 (trans[S][a]=1) 已经存在。
不失一般性,我们可以认为在 ( ext{suffix-path}(u ightarrow S)) 遇到的第一个状态v满足 (trans[v][S[i+1]]=x)。这时我们需要讨论 (x) 包含的子串的情况。如果 (x) 中包含的最长子串就是v中包含的最长子串接上字符S[i+1],等价于maxlen(v)+1=maxlen(x),比如在上面的例子里,(v=S, x=1),(longest(v)) 是空串,(longest(1)="a") 就是 (longest(v)+'a')。这种情况比较简单,我们只要增加 (slink[z]=x) 即可。
如果(x) 中包含的最长子串不是 (v) 中包含的最长子串接上字符 (S[i+1]),等价于 (maxlen(v)+1 < maxlen(x)),这种情况最为复杂,不失一般性,用下图表示这种情况,这时增加的字符是 (c),状态是 (z)。

在 ( ext{suffix-path}(u ightarrow S)) 这条路径上,从u开始有一部分连续的状态满足 (trans[u..][c]=NULL),对于这部分状态我们只需增加 (trans[u..][c]=z)。紧接着有一部分连续的状态 (v..w) 满足 (trans[v..w][c]=x),并且 (longest(v)+c) 不等于 (longest(x))。这时我们需要从 (x) 拆分出新的状态 (y),并且把原来 (x) 中长度小于等于 (longest(v)+c) 的子串分给 (y),其余字串留给 (x)。同时令 (trans[v..w][c]=y),(slink[y]=slink[x], slink[x]=slink[z]=y)。
举个例子。假设我们已经构造 ("aab") 的 ( ext{SAM}) 如图,现在我们要增加一个字符 (b) 构造 ("aabb") 的( ext{SAM})。
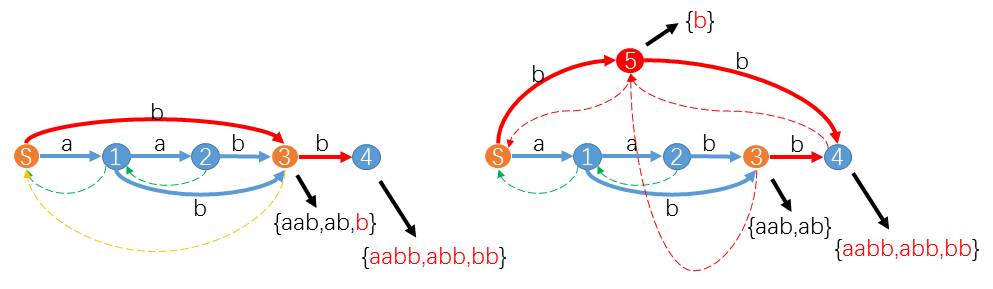
当我们处理在 ( ext{suffix-path}(u ightarrow S)) 上的状态 (S) 时,遇到 (trans[S][b]=3)。并且 (longest(3)="aab"),(longest(S)+'b'="b"),两者不相等。其实不相等意味增加了新字符后 (endpos("aab")) 已经不等于 (endpos("b")),势必这两个子串不能同属一个状态 (3)。这时我们就要从 (3) 中新拆分出一个状态 (5),把 ("b")及其后缀分给 (5),其余的子串留给 (3)。同时令 (trans[S][b]=5, slink[5]=slink[3]=S, slink[3]=slink[4]=5)。
此处加入一些个人理解:对于一条 ( ext{suffix-path}(u ightarrow S)) 所包含的所有子串,其必然是连续的,也就是说,在路径上的同一个状态里内的子串,(append) 字符 (S[i+1]) 之后其 (endpos) 集合都还是相等的。然后考虑当某个状态已经有了字符 (S[i+1]) 的转移时,若对应 (append) 字符 (S[i+1]) 后所对应的子串其所在的状态的等价类最长的字符串,那么由于比它长的串都必定不在 ( ext{suffix-path}(u ightarrow S)) 上的同一个状态内,所以它们的 (endpos)$ 集合也必定已经不同。