红黑树原理

定义

    节点有红黑属性,非黑即红

    根节点为黑色

    两个相邻节点不能同时为红色(若同时红色触发recolor或rotation),相邻节点可以是黑色

    能保证节点到任意子节点的null节点路径中经过的黑色节点个数相同

 

平衡方式

    重标色recolor + 旋转rotation

    新插入节点X

        若X是根节点则标为黑色

        若非根节点则按照二叉树规则插入,并标为红色

            若父节点P为黑色,则结束

            若父节点P为红色

                若叔叔节点U为红色 -> recolor: P-黑,U-黑, G-红

                若叔叔节点U为黑色,再判断X与P的位置关系

                    若左左  -> rotation:右旋,  recolor:X-红,G-红,P-黑

                    若右右  -> rotation:左旋,  recolor:X-红,G-红,P-黑

                    若左右  -> rotation: 先左旋,再右旋  recolor:X-黑,G-红,P-红

                    若右左  -> rotation: 先右旋,再左旋  recolor:X-黑,G-红,P-红

 

 

下图为左左情况

 

 

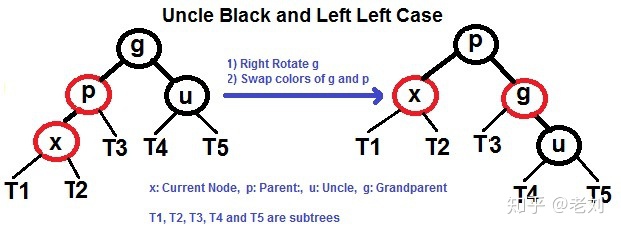
下图为左右情况

 

与平衡二叉树对比

    二者都是平衡的二叉树, AVLTree相对于RBTree是更严格的平衡树

    二者触发平衡动作的因子不同,RBTree是相邻节点都是红色, AVLTree是节点平衡因>1.但二者旋转算法是一样的, 所以先搞懂AVLTree后就比较好理解RBTree了

    由于RBTree不是强平衡,所以树的新增和删除旋转的次数相对少一些.另外通过节点的红黑关系来确定旋转,少了AVLTree递归计算深度.在插入和删除性能上RBTree更优.但是查询没有AVLTree高效和稳定;

 

应用场景

    AVLTree目前应用于WindowsNT

    RBTree应用在HashMap