[Codeforces 15E] Triangle

Brief Introduction:

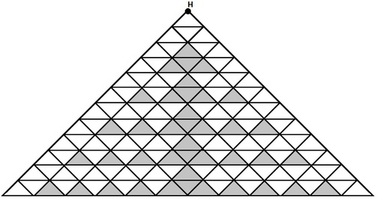
求从N出发，回到N且不包含任何黑色三角的路径数

Algorithm:
假设从N点到第二层中间的节点M的路径数为k，易知总路径数为(k*k+1)*2

而从第第四层开始，每两行之间的形状是具有规律的，我们称之为一个“凹槽”。

每个“凹槽”的方案数是具有规律的：2n-2到2n间的方案数F(n)=2^n-3（不考虑从最外层跳到次外层）

所以到恰好到第2n层的总方案数S(n)=4*F(3)*F(4)......*F(n)，res=6+S(3)+S(4)....+S(n)

由于一共只能从最外层跳一次到次外层，所以将4乘出来

Code:

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int MOD=1e9+9;

int main()
{
    int n;cin >> n;
    
    if(n==2) return cout << 10,0;
    
    ll a=4,cur=4,res=6;
    for(int i=3;i<=n/2;i++)
        a=a*2%MOD,cur=(cur*(a-3+MOD))%MOD,res=(res+cur)%MOD;
    cout << 2*(res*res+1)%MOD;
    return 0;
}

Review:

1、找到位置转移的一些规律（只能跳跃一次），将转换的方式另外乘出来即可

2、发现递进性的规律，大胆推公式，注意好初始化与特解即可