激活函数及其梯度

目录

• Activation Functions
  • Derivative
• Sigmoid/Logistic
  • Derivative
  • tf.sigmoid
• Tanh
  • Derivative
  • tf.tanh
• Rectified Linear Unit
  • Derivative
  • tf.nn.relu

Activation Functions

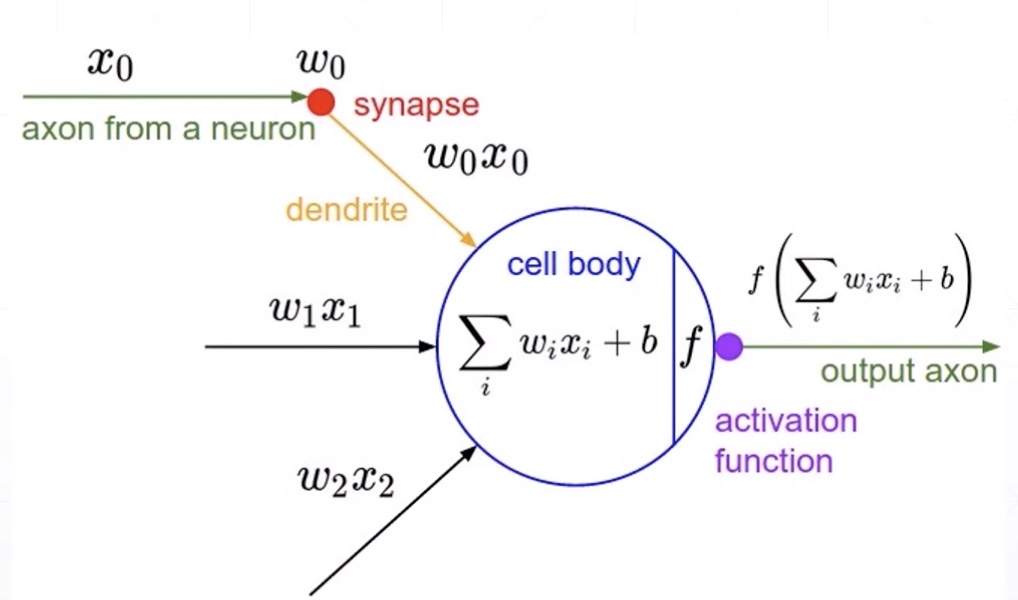
Derivative

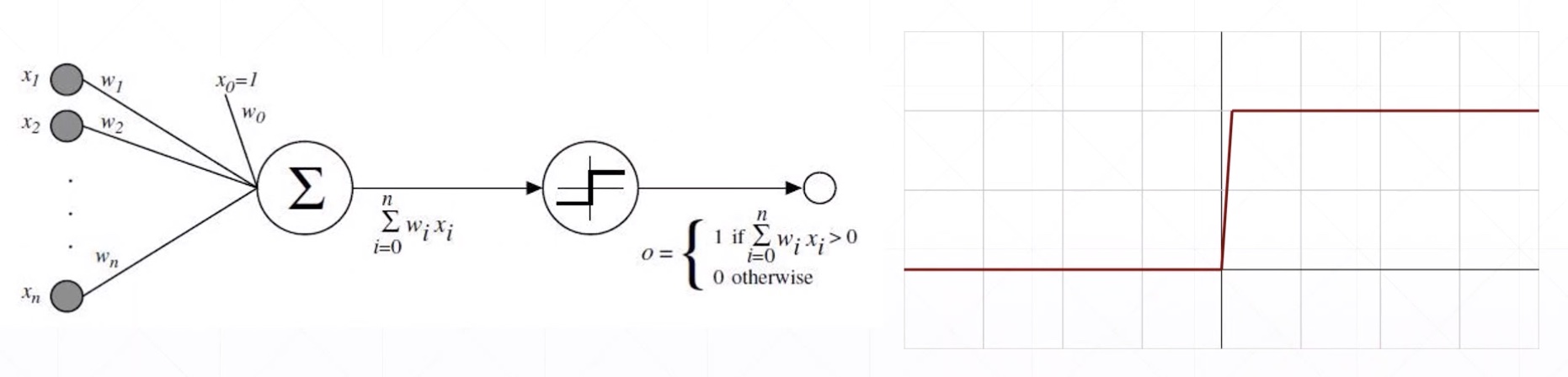
Sigmoid/Logistic

• (f(x)=sigma{(x)}=frac{1}{1+e^{-x}})

• 把((-infty,+infty))的值压缩在0-1之间

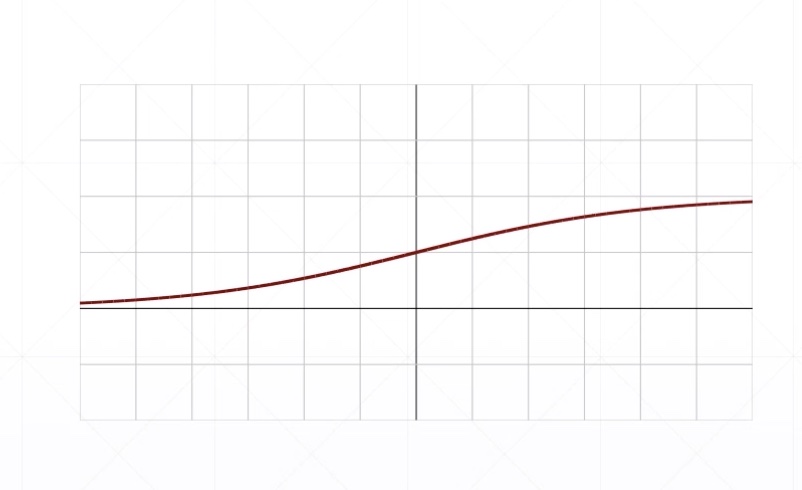
Derivative

[frac{d}{dx}sigma(x)=frac{d}{dx}(frac{1}{1+e^{-x}})=sigma(x)-sigma(x)^2 ]

• 由上式可得到(sigma^{'}=sigma(1-sigma))

• 由于x较大时sigmoid的偏导为0，所以参数得不到更新，此时则会有梯度消失现象发生。

tf.sigmoid

import tensorflow as tf

a = tf.linspace(-10., 10., 10)
a

<tf.Tensor: id=17, shape=(10,), dtype=float32, numpy=
array([-10.       ,  -7.7777777,  -5.5555553,  -3.333333 ,  -1.1111107,
         1.1111116,   3.333334 ,   5.5555563,   7.7777786,  10.       ],
      dtype=float32)>

with tf.GradientTape() as tape:
    tape.watch(a)
    y = tf.sigmoid(a)

y

<tf.Tensor: id=19, shape=(10,), dtype=float32, numpy=
array([4.5418739e-05, 4.1875243e-04, 3.8510859e-03, 3.4445167e-02,
       2.4766389e-01, 7.5233626e-01, 9.6555483e-01, 9.9614894e-01,
       9.9958128e-01, 9.9995458e-01], dtype=float32)>

grads = tape.gradient(y, [a])
grads

[<tf.Tensor: id=24, shape=(10,), dtype=float32, numpy=
 array([4.5416677e-05, 4.1857705e-04, 3.8362551e-03, 3.3258699e-02,
        1.8632649e-01, 1.8632641e-01, 3.3258699e-02, 3.8362255e-03,
        4.1854731e-04, 4.5416677e-05], dtype=float32)>]

Tanh

[f(x) = tanh(x) = frac{e^x-e^{-x}}{e^x+e^{-x}}=2sigmoid(2x)-1 ]

• 类似于sigmoid函数，但是值域为[-1,1]

Derivative

[frac{d}{dx}tanh(x)=1-tanh^2(x) ]

tf.tanh

a = tf.linspace(-5.,5.,10)
a

<tf.Tensor: id=29, shape=(10,), dtype=float32, numpy=
array([-5.        , -3.8888888 , -2.7777777 , -1.6666665 , -0.55555534,
        0.5555558 ,  1.666667  ,  2.7777781 ,  3.8888893 ,  5.        ],
      dtype=float32)>

tf.tanh(a)

<tf.Tensor: id=31, shape=(10,), dtype=float32, numpy=
array([-0.99990916, -0.9991625 , -0.99229795, -0.9311096 , -0.5046722 ,
        0.5046726 ,  0.93110967,  0.99229795,  0.9991625 ,  0.99990916],
      dtype=float32)>

Rectified Linear Unit

[f(x)= egin{cases} 0\,\,for\,x<0 \ x\,\,for\,xgeq{0} end{cases} ]

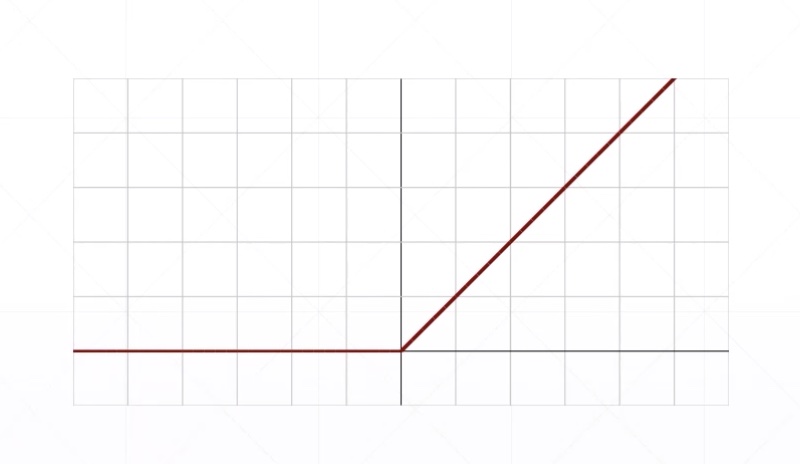
Derivative

[f'(x)= egin{cases} 0\,\,for\,x<0 \ 1\,\,for\,xgeq{0} end{cases} ]

• 减少sigmoid的梯度爆炸或者梯度消失的现象

tf.nn.relu

a = tf.linspace(-1.,1.,10)
a

<tf.Tensor: id=36, shape=(10,), dtype=float32, numpy=
array([-1.        , -0.7777778 , -0.5555556 , -0.3333333 , -0.1111111 ,
        0.11111116,  0.33333337,  0.5555556 ,  0.7777778 ,  1.        ],
      dtype=float32)>

tf.nn.relu(a)

<tf.Tensor: id=38, shape=(10,), dtype=float32, numpy=
array([0.        , 0.        , 0.        , 0.        , 0.        ,
       0.11111116, 0.33333337, 0.5555556 , 0.7777778 , 1.        ],
      dtype=float32)>

tf.nn.leaky_relu(a)

<tf.Tensor: id=40, shape=(10,), dtype=float32, numpy=
array([-0.2       , -0.15555556, -0.11111112, -0.06666666, -0.02222222,
        0.11111116,  0.33333337,  0.5555556 ,  0.7777778 ,  1.        ],
      dtype=float32)>