1. 项目要求
1.1 要求阐述
- 生成小学四则运算题题目,结果不能为负数
- 支持真分数的四则运算
1.2 详细要求 【易知大学】
1.3 详细代码 【GitHub】
2. PSP表格
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
15 |
25 |
|
Estimate |
估计这个任务需要多少时间 |
15 |
25 |
|
Development |
开发 |
247 |
395 |
|
Analysis |
需求分析 (包括学习新技术) |
30 |
45 |
|
Design Spec |
生成设计文档 |
30 |
30 |
|
Design Review |
设计复审 (和同事审核设计文档) |
15 |
10 |
|
Coding Standard |
代码规范 (为目前的开发制定合适的规范) |
12 |
10 |
|
Design |
具体设计 |
30 |
35 |
|
Coding |
具体编码 |
60 |
180 |
|
Code Review |
代码复审 |
30 |
20 |
|
Test |
测试(自我测试,修改代码,提交修改) |
40 |
65 |
|
Reporting |
报告 |
85 |
60 |
|
Test Report |
测试报告 |
30 |
25 |
|
Size Measurement |
计算工作量 |
30 |
10 |
|
Postmortem & Process Improvement Plan |
事后总结, 并提出过程改进计划 |
25 |
25 |
|
合计 |
347 |
480 |
3. 解题思路描述
将问题分解为两部分:第一部分生成算式,第二部分计算算式的值。
3.1 第一部分
生成算式分为三个小步骤。
首先,使用随机数生成操作数与运算符,通过参数设置操作数与运算符的数量,再将其拼接为算式,如3×7+9÷3。
其次,在算式上插入括号,括号插在有乘除附近的加减子算式中,如3×(7+9)÷3。
最后,在算式的基础上将其中的数字替换为分数,如果不想使用分数则跳过此步骤。
3.2 第二部分
计算算式的值,将算式转为逆波兰式,之后使用栈计算算式结果,结果保留分数形式,如7/2。
4. 设计实现过程
4.1 参数说明
创建OPT方法存储相关参数,如操作数数值上限、操作数个数、使用的运算符种类、是否包含分数。
4.2 生成算式
使用GeneralFormular类生成算式的中缀表达式,其中包含8个方法。
|
|
方法 |
说明 |
|
1 |
def catFormula(self, operand1, operator, operand2) |
连接算式 |
|
2 |
def getRandomIntOperand(self) |
返回随机整数操作数 |
|
3 |
def getRandomFractionOperand(self) |
返回随机分数操作数 |
|
4 |
def getRandomOperator(self) |
返回随机运算符 |
|
5 |
def getOriginFormular(self) |
生成整数源算式 |
|
6 |
def insertBracket(self, formular) |
插入括号 |
|
7 |
def replaceFraction(self, formular) |
带入分数 |
|
8 |
def solve(self) |
整合生成算式的后缀表达式,带括号 |
4.3 计算算式
使用ComputeFormular类计算算式,通过将中缀表达式转为后缀表达式,使用栈计算结果。
|
|
方法 |
说明 |
|
1 |
def getPostFormular(self, formular) |
中缀表达式转为后缀表达式 |
|
2 |
def calcFormular(self, formular) |
计算算式的值 |
|
3 |
def solve(self, formular) |
整合计算中缀表达式的值 |
5. 代码示例
5.1 opt()方法
1 def OPT(up_limit=10, oper_num=2, oper_variety=4, has_fraction=True):
2 '''
3 * 设置参数
4
5 * @param up_limit {int} 操作数数值上限
6
7 * @param oper_num {int} 操作数个数
8
9 * @param oper_variety {int} 运算符种类
10
11 * @param has_fraction {bool} 是否带有分数
12 '''
13 parse = argparse.ArgumentParser()
14 # 操作数数值上限
15 parse.add_argument('--up_limit', type=int, default=up_limit)
16 # 操作数个数
17 parse.add_argument('--oper_num', type=int, default=oper_num)
18 # 运算符种类
19 parse.add_argument('--oper_variety', type=int, default=oper_variety)
20 # 是否带有分数
21 parse.add_argument('--has_fraction', type=bool, default=has_fraction)
22
23 return parse.parse_args(args=[])
5.2 GeneralFormular.getOriginFormular()方法
def getOriginFormular(self):
'''
* 生成整数源算式
* @return {str}
'''
# 通过self.opt.oper_num控制操作数个数,循环调用catFormula()方法构造算式
tmp = self.getRandomIntOperand()
for i in range(self.opt.oper_num-1):
tmp = self.catFormula(tmp, self.getRandomOperator(), self.getRandomIntOperand())
# 去掉'÷0'
while(True):
if '÷0' in tmp:
tmp = tmp.replace('÷0', '÷'+str(self.getRandomIntOperand()))
else:
break
return tmp
5.3 GeneralFormular.insertBracket()方法
1 def insertBracket(self, formular):
2 '''
3 * 插入括号
4
5 * @param formular {str} 源算式
6
7 * @return {str}
8 '''
9 # 若只包含+号 或 只有两个操作数 则不用加括号
10 if self.opt.oper_variety <= 2 or self.opt.oper_num == 2:
11 return formular
12 # 若不包含×÷ 则不用加括号
13 if '×' not in formular and '÷' not in formular:
14 return formular
15
16 # 操作数列表
17 operand_list = re.split("[-|+|×|÷]", formular)
18 # 操作符列表
19 operator_list = re.split("[!0-9]", formular)
20 # 去掉空字符
21 while '' in operator_list:
22 operator_list.remove('')
23 # print(operand_list, operator_list)
24
25 # 存储添加括号的算式
26 new_formular = ""
27
28 # flag表示是否已存在左括号,作用在于构造出一对括号
29 flag = 0
30
31 # 添加括号
32 for i in range(len(operator_list)):
33 oper = operator_list.pop(0)
34 # 若下一个符号为 + or - , 则插入括号
35 if oper == '-' or oper == '+':
36 if flag == 0:
37 new_formular += "("
38 flag = 1
39 new_formular += (str(operand_list.pop(0)) + str(oper))
40 else:
41 new_formular += str(operand_list.pop(0))
42
43 if flag == 1:
44 new_formular += ")"
45 flag = 0
46
47 new_formular += str(oper)
48 # print(operand_list, operator_list, new_formular)
49
50 new_formular += str(operand_list.pop(0))
51 if flag == 1:
52 new_formular += ")"
53
54 return new_formular
6. 测试运行
6.1 运行代码
1 from formula import OPT, GeneralFormular, ComputeFormular
2
3 if __name__ == "__main__":
4 print("{:^18} | {:^5} | {:^8}".format("参数", "数值范围", "请输入"))
5 print("{0:-<21}+{0:-<11}+{0:-<12}".format('-'))
6 n = input("{:>14} | {:9} | ".format("生成算式数量", "[>=1]"))
7 up_limit = input("{:>16} | {:9} | ".format("数值上限", "[>=10]"))
8 oper_num = input("{:>15} | {:9} | ".format("操作数个数", "[>=2]"))
9 oper_variety = input("{:>15} | {:9} | ".format("运算符种数", "[1~4]"))
10 has_fraction = int(input("{:>14} | {:9} | ".format("是否包含分数", "[0, 1]")))
11 print("{0:-<46}".format('-'))
12 opt = OPT(up_limit, oper_num, oper_variety, has_fraction)
13
14 gf = GeneralFormular(opt)
15 cf = ComputeFormular()
16
17 formulars = {}
18 for i in range(int(n)):
19 f = gf.solve()
20 s = cf.solve(f)
21 formulars[i+1] = f + " = " + s
22 print(formulars[i+1])
6.2 不包含分数、包含加减

6.3 不包含分数、包含加减乘

6.4 包含分数、包含加减乘除
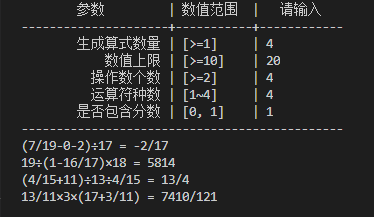
7. 单元测试
1 import unittest
2 from formula import OPT, GeneralFormular, ComputeFormular
3
4 class FormulaUnitTest(unittest.TestCase):
5 def test_gf_catFormular(self):
6 '''
7 * 测试拼接算式
8 '''
9 gf = GeneralFormular(OPT())
10 self.assertEqual(gf.catFormula("12", "+", "34"), "12+34")
11 self.assertEqual(gf.catFormula("23", "+", "456"), "23+456")
12 self.assertEqual(gf.catFormula("1z", "+", "32"), "1z+32")
13
14 def test_cf_getPostFormular(self):
15 '''
16 * 测试中缀表达式转为后缀表达式
17 '''
18 cf = ComputeFormular()
19 self.assertEqual(cf.getPostFormular("3+7"), "3#7#+")
20 self.assertEqual(cf.getPostFormular("3×(7+2+1)"), "3#7#2#+1#+×")
21 self.assertEqual(cf.getPostFormular("6×(2+1)÷(9-2+3)"), "6#2#1#+×9#2#-3#+÷")
22 self.assertEqual(cf.getPostFormular("6×(2+1)÷0"), "6#2#1#+×0#÷")
23
24 def test_cf_calcFormular(self):
25 '''
26 * 测试后缀表达式计算为数值
27 '''
28 cf = ComputeFormular()
29 self.assertEqual(cf.calcFormular("3#7#+"), "10")
30 self.assertEqual(cf.calcFormular("3#7#2#+1#+×"), "30")
31 self.assertEqual(cf.calcFormular("6#2#1#+×9#2#-3#+÷"), "9/5")
32 self.assertEqual(cf.calcFormular("6#2#1#+×0#÷"), "NaN")
33
34
35 if __name__ == "__main__":
36 unittest.main()
