计蒜客：网络交友：map+set+并查集

　　在网络社交的过程中，通过朋友，也能认识新的朋友。在某个朋友关系图中，假定 A 和 B 是朋友，B 和 C 是朋友，那么 A 和 C 也会成为朋友。即，我们规定朋友的朋友也是朋友。

现在要求你每当有一对新的朋友认识的时候，你需要计算两人的朋友圈合并以后的大小。

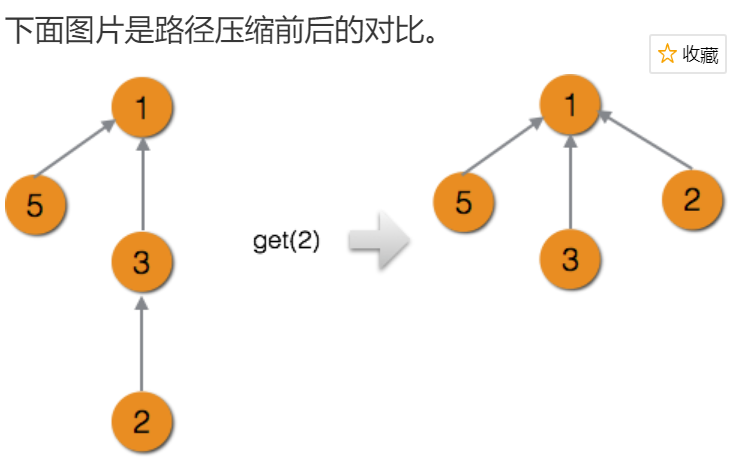
解决思想：

路径压缩：只关心每个结点的父结点，而不关心树的真正结构，在一次查询过程中，把查找路径上的结点的父结点都设为根结点

1.set来存储人名字（实质上是用来人名去重，是一个辅助手段）

2.经过set去重，map来存储名字和编号num++

3.while循环里边输入边统计

#include <iostream>
#include <map>
#include <set>
using namespace std;
int  pa[10010];//
void init(){//每个元素都是一个集合，自己是自己的根结点
    for(int i=1;i<=10000;i++){
        pa[i]=i;
    }
}
int get(int x){//路径压缩思想查找
    if(pa[x]==x){
        return x;
    }
    return pa[x]=get(pa[x]);
}
int merge(int x,int y){
    int fx=pa[x];
    int fy=pa[y];
    if(fx!=fy){
        pa[fx]=fy;
    }
}
int main(){
    int n;
    cin>>n;
    set<string> name;
    map<string,int> m;
    int num=1;
    init();
    string a,b;
    while(n--){
        cin>>a>>b;
        if(!name.count(a)){//名字a没出现过在name中
            name.insert(a);
            m[a]=num++;//先赋值后加1
        }
        if(!name.count(b)){//同上判断b
            name.insert(b);
            m[b]=num++;
        }
        merge(m[a],m[b]);//用map的编号 关联a，b
        int res=0;
        for(int i=1;i<num;i++){
            if(get(i)==get(m[b]))//get时已经压缩路径，此处是从头查找和m[b]同一根结点的结点个数，并输出
                res++;
        }
        cout<<res<<endl;
    }
     return 0;  
}