数据结构和算法(Golang实现)(12)常见数据结构-链表

zoukankan html css js c++ java

数据结构和算法(Golang实现)(12)常见数据结构-链表
链表

讲数据结构就离不开讲链表。因为数据结构是用来组织数据的，如何将一个数据关联到另外一个数据呢？链表可以将数据和数据之间关联起来，从一个数据指向另外一个数据。

一、链表

定义：

链表由一个个数据节点组成的，它是一个递归结构，要么它是空的，要么它存在一个指向另外一个数据节点的引用。

链表，可以说是最基础的数据结构。

最简单的链表如下：
```
package main

import (
    "fmt"
)

type LinkNode struct {
    Data     int64
    NextNode *LinkNode
}

func main() {
    // 新的节点
    node := new(LinkNode)
    node.Data = 2

    // 新的节点
    node1 := new(LinkNode)
    node1.Data = 3
    node.NextNode = node1 // node1 链接到 node 节点上

    // 新的节点
    node2 := new(LinkNode)
    node2.Data = 4
    node1.NextNode = node2 // node2 链接到 node1 节点上

    // 按顺序打印数据
    nowNode := node
    for {
        if nowNode != nil {
            // 打印节点值
            fmt.Println(nowNode.Data)
            // 获取下一个节点
            nowNode = nowNode.NextNode
        }

        // 如果下一个节点为空，表示链表结束了
        break
    }
}
```
打印出：
```
2
3
4
```
结构体LinkNode有两个字段，一个字段存放数据Data，另一个字典指向下一个节点NextNode。这种从一个数据节点指向下一个数据节点的结构，都可以叫做链表。

有些书籍，把链表做了很细的划分，比如单链表，双链表，循环单链表，循环双链表，其实没有必要强行分类，链表就是从一个数据指向另外一个数据，一种将数据和数据关联起来的结构而已。

好吧，我们还是要知道是什么。
1. 单链表，就是链表是单向的，像我们上面这个结构一样，可以一直往下找到下一个数据节点，它只有一个方向，它不能往回找。
2. 双链表，每个节点既可以找到它之前的节点，也可以找到之后的节点，是双向的。
3. 循环链表，就是它一直往下找数据节点，最后回到了自己那个节点，形成了一个回路。循环单链表和循环双链表的区别就是，一个只能一个方向走，一个两个方向都可以走。
我们来实现一个循环链表Ring（集链表大成者），参考Golang标准库container/ring：：
```
// 循环链表
type Ring struct {
    next, prev *Ring       // 前驱和后驱节点
    Value      interface{} // 数据
}
```
该循环链表有一个三个字段，next表示后驱节点，prev表示前驱节点，Value表示值。

我们来分析该结构各操作的时间复杂度。

1.1.初始化循环链表

初始化一个空的循环链表：
```
package main

import (
    "fmt"
)

// 初始化空的循环链表，前驱和后驱都指向自己，因为是循环的
func (r *Ring) init() *Ring {
    r.next = r
    r.prev = r
    return r
}


func main() {
    r := new(Ring)
    r.init()
}
```
因为绑定前驱和后驱节点为自己，没有循环，时间复杂度为：O(1)。

创建一个指定大小N的循环链表，值全为空：
```
// 创建N个节点的循环链表
func New(n int) *Ring {
    if n <= 0 {
        return nil
    }
    r := new(Ring)
    p := r
    for i := 1; i < n; i++ {
        p.next = &Ring{prev: p}
        p = p.next
    }
    p.next = r
    r.prev = p
    return r
}
```
会连续绑定前驱和后驱节点，时间复杂度为：O(n)。

1.2.获取上一个或下一个节点
```
// 获取下一个节点
func (r *Ring) Next() *Ring {
    if r.next == nil {
        return r.init()
    }
    return r.next
}

// 获取上一个节点
func (r *Ring) Prev() *Ring {
    if r.next == nil {
        return r.init()
    }
    return r.prev
}
```
获取前驱或后驱节点，时间复杂度为：O(1)。

1.2.获取第 n 个节点

因为链表是循环的，当n为负数，表示从前面往前遍历，否则往后面遍历：
```
func (r *Ring) Move(n int) *Ring {
    if r.next == nil {
        return r.init()
    }
    switch {
    case n < 0:
        for ; n < 0; n++ {
            r = r.prev
        }
    case n > 0:
        for ; n > 0; n-- {
            r = r.next
        }
    }
    return r
}
```
因为需要遍历n次，所以时间复杂度为：O(n)。

1.3.添加节点
```
// 往节点A，链接一个节点，并且返回之前节点A的后驱节点
func (r *Ring) Link(s *Ring) *Ring {
    n := r.Next()
    if s != nil {
        p := s.Prev()
        r.next = s
        s.prev = r
        n.prev = p
        p.next = n
    }
    return n
}
```
添加节点的操作比较复杂，如果节点s是一个新的节点。

那么也就是在r节点后插入一个新节点s，而r节点之前的后驱节点，将会链接到新节点后面，并返回r节点之前的第一个后驱节点n，图如下：

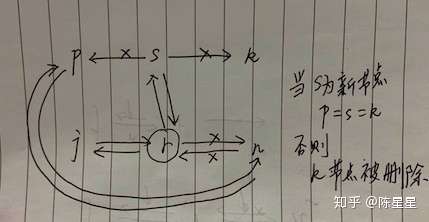
可以看到插入新节点，会重新形成一个环，新节点s被插入了中间。

执行以下程序：
```
package main

import (
    "fmt"
)

ffunc linkNewTest() {
     // 第一个节点
     r := &Ring{Value: -1}

     // 链接新的五个节点
     r.Link(&Ring{Value: 1})
     r.Link(&Ring{Value: 2})
     r.Link(&Ring{Value: 3})
     r.Link(&Ring{Value: 4})

     node := r
     for {
         // 打印节点值
         fmt.Println(node.Value)

         // 移到下一个节点
         node = node.Next()

         //  如果节点回到了起点，结束
         if node == r {
             return
         }
     }
 }

func main() {
    linkNewTest()
}
```
输出:
```
-1
4
3
2
1
```
每次链接的是一个新节点，那么链会越来越长，仍然是一个环。因为只是更改链接位置，时间复杂度为：O(1)。

1.4.删除节点
```
// 删除节点后面的 n 个节点
func (r *Ring) Unlink(n int) *Ring {
    if n < 0 {
        return nil
    }
    return r.Link(r.Move(n + 1))
}
```
将循环链表的后面几个节点删除。

执行：
```
package main

import (
    "fmt"
)

func deleteTest() {
    // 第一个节点
    r := &Ring{Value: -1}

    // 链接新的五个节点
    r.Link(&Ring{Value: 1})
    r.Link(&Ring{Value: 2})
    r.Link(&Ring{Value: 3})
    r.Link(&Ring{Value: 4})

    temp := r.Unlink(3) // 解除了后面两个节点

    // 打印原来的节点
    node := r
    for {
        // 打印节点值
        fmt.Println(node.Value)
        // 移到下一个节点
        node = node.Next()

        //  如果节点回到了起点，结束
        if node == r {
            break
        }
    }

    fmt.Println("------")

    // 打印被切断的节点
    node = temp
    for {
        // 打印节点值
        fmt.Println(node.Value)
        // 移到下一个节点
        node = node.Next()

        //  如果节点回到了起点，结束
        if node == temp {
            break
        }
    }
}

func main() {
    deleteTest()
}
```
输出：
```
-1
1
------
4
3
2
```
删除循环链表后面的三个节点：r.Unlink(3)。

可以看到节点r后面的两个节点被切断了，然后分成了两个循环链表，r所在的链表变成了-1，1。

而切除的那部分形成一个新循环链表是4 3 2，并且返回给了用户。

因为只要定位要删除的节点位置，然后进行链接：r.Link(r.Move(n + 1))，所以时间复杂度为：O(n)+O(1)=O(n)

1.5.获取链表长度
```
// 查看循环链表长度
func (r *Ring) Len() int {
    n := 0
    if r != nil {
        n = 1
        for p := r.Next(); p != r; p = p.next {
            n++
        }
    }
    return n
}
```
通过循环，当引用回到自己，那么计数完毕，时间复杂度：O(n)。

因为循环链表还不够强壮，不知道起始节点是哪个，计数链表长度还要遍历，所以用循环链表实现的双端队列就出现了，一般具体编程都使用更高层次的数据结构。

详细可查看栈和队列章节。

二、数组和链表

数组是编程语言作为一种基本类型提供出来的，相同数据类型的元素按一定顺序排列的集合。

它的作用只有一种：存放数据，让你很快能找到存的数据。如果你不去额外改进它，它就只是存放数据而已，它不会将一个数据节点和另外一个数据节点关联起来。比如建立一个大小为5的数组array:
```
package main

import "fmt"


//  打印出：
//  [0 0 0 0 0]
//  [8 9 7 0 0]
//  7
func main() {
    array := [5]int64{}
    fmt.Println(array)
    array[0] = 8
    array[1] = 9
    array[2] = 7
    fmt.Println(array)
    fmt.Println(array[2])
}
```
我们可以通过下标0，1，2来获取到数组中的数据，下标0，1，2就表示数据的位置，排第一位，排第二位，我们也可以把指定位置的数据替换成另外一个数据。

数组这一数据类型，是被编程语言高度抽象封装的结构，下标会转换成虚拟内存地址，然后操作系统会自动帮我们进行寻址，这个寻址过程是特别快的，所以往数组的某个下标取一个值和放一个值，时间复杂度都为O(1)。

它是一种将虚拟内存地址和数据元素映射起来的内置语法结构，数据和数据之间是挨着，存放在一个连续的内存区域，每一个固定大小（8字节）的内存片段都有一个虚拟的地址编号。当然这个虚拟内存不是真正的内存，每个程序启动都会有一个虚拟内存空间来映射真正的内存，这是计算机组成的内容，和数据结构也有点关系，我们会在另外的高级专题讲，这里就不展开了。

用数组也可以实现链表，比如定义一个数组[5]Value，值类型为一个结构体Value：
```
package main

import "fmt"

func ArrayLink() {
    type Value struct {
        Data      string
        NextIndex int64
    }

    var array [5]Value          // 五个节点的数组
    array[0] = Value{"I", 3}    // 下一个节点的下标为3
    array[1] = Value{"Army", 4} // 下一个节点的下标为4
    array[2] = Value{"You", 1}  // 下一个节点的下标为1
    array[3] = Value{"Love", 2} // 下一个节点的下标为2
    array[4] = Value{"!", -1}   // -1表示没有下一个节点
    node := array[0]
    for {
        fmt.Println(node.Data)
        if node.NextIndex == -1 {
            break
        }
        node = array[node.NextIndex]
    }

}

func main() {
    ArrayLink()
}
```
打印出：
```
I
Love
You
Army
!
```
获取某个下标的数据，通过该数据可以知道下一个数据的下标是什么，然后拿出该下标的数据，继续往下做。问题是，有时候需要做删除，移动等各种操作，而数组的大小是固定的，需要大量空间移动，所以某些情况下，数组的效率很低。

数组和链表是两个不同的概念。一个是编程语言提供的基本数据类型，表示一个连续的内存空间，可通过一个索引访问数据。另一个是我们定义的数据结构，通过一个数据节点，可以定位到另一个数据节点，不要求连续的内存空间。

数组的优点是占用空间小，查询快，直接使用索引就可以获取数据元素，缺点是移动和删除数据元素要大量移动空间。

链表的优点是移动和删除数据元素速度快，只要把相关的数据元素重新链接起来，但缺点是占用空间大，查找需要遍历。

很多其他的数据结构都由数组和链表配合实现的。

三、总结

链表和数组可以用来辅助构建各种基本数据结构。

数据结构名字特别多，在以后的计算机生涯中，有些自己造的数据结构，或者不常见的别人造的数据结构，不知道叫什么名字是很正常的。我们只需知道常见的数据结构即可，方便与其他程序员交流。

系列文章入口

我是陈星星，欢迎阅读我亲自写的 数据结构和算法(Golang实现)，文章首发于阅读更友好的GitBook。
查看全文

相关阅读:
Leetcode题目322.零钱兑换（动态规划-中等）
Leetcode题目292.Nim游戏（脑筋急转弯）
Leetcode题目300.最长上升子序列（动态规划-中等）
Leetcode题目287.寻找重复数（中等）
Android学习笔记---初识eventbus
Android学习笔记----实现卡牌翻转动画
 Android学习笔记----在Android使用ping来检测网络是否可用
 Android学习笔记----初体验ButterKnife框架
 Android 学习笔记---使用shell命令来关闭和开启ADB
Android学习笔记--客户端上传图片到PHP服务器（带PHP端代码）

原文地址：https://www.cnblogs.com/nima/p/12724826.html

数据结构和算法(Golang实现)(12)常见数据结构-链表

链表

一、链表

1.1.初始化循环链表

1.2.获取上一个或下一个节点

1.2.获取第 n 个节点

1.3.添加节点

1.4.删除节点

1.5.获取链表长度

二、数组和链表

三、总结

系列文章入口