定义
小于n的正整数中与n互质的数的数目(φ(1)=1)
通式
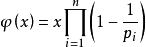
证明:
设p是N的质因子,1~N中p的倍数有p,2p,3p,…,(N/p)*p,共N/p个。
同理,若q也是N的质因子,则1~N中q的倍数有N/q个。
根据容斥原理,1~N中除去q的倍数与p的倍数后,数的个数为N - N/p - N/q + N/(pq) = N(1 - 1/p)(1 - 1/q)。
而要求1~N中与N互质的数的个数,只需将N的所有质因子的倍数全部除去即可。
利用容斥原理,因式分解后即可得到上式。
性质
(以下只列举我们需要用到的一些性质)
我们用phi(N)表示欧拉函数。
- 当N为质数时,显然phi(N)=N-1。
- 2.根据算数基本定理,N=p1C1*p2C2*…*pkCk 。设N的最小质因子为p,当p的指数为1时,phi(N)=(p-1)*phi(N/p)。
- 3. 当p的指数不为1时,同2可证得phi(N)=p*phi(N/p)。
2的证明:
根据欧拉函数通式,
phi(N)=N*(p1-1)/p1*(p2-1)/p2*…*(pk-1)/pk,
phi(N/p1)=N/p1*(p2-1)/p2*…*(pk-1)/pk,
其中p1即为N的最小质因子,比较两式即可得证。
直接法
模板题链接:欧拉函数
代码实现:
int Euler(int x) { int res=x;for(int i=2;i<=x/i;i++) { if(x%i==0) { res=res/i*(i-1); while(x%i==0)x/=i; } } if(x>1)res=res/x*(x-1); return res; }
线性筛法
根据前面的欧拉线性筛质数的算法(可参考本人博客:数论——质数筛法),由于它在筛选的同时也求出了每个数的最小质因子,故而在其基础上求出欧拉函数即可。
模板题链接:筛法求欧拉函数
代码如下:
typedef long long ll; const int N = 1000010; int n; int prime[N],cnt,v[N]; int phi[N]; ll Euler_prime(int n) { phi[1]=1; for(int i=2;i<=n;i++) { if(!v[i]) { prime[++cnt]=i; phi[i]=i-1; } for(int j=1;prime[j]<=n/i;j++) { int p=prime[j]; v[p*i]=1; if(i%prime[j]==0) { phi[i*p]=p*phi[i]; break; } phi[i*p]=(p-1)*phi[i]; } } ll res=0; for(int i=1;i<=n;i++)res+=phi[i]; return res; }