岭回归的原理:
首先要了解最小二乘法的回归原理
设有多重线性回归模型 y=Xβ+ε ,参数β的最小二乘估计为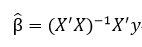
当自变量间存在多重共线性,|X'X|≈0时,设想|X'X|给加上一个正常数矩阵(k>0)
那么|X'X|+kI 接近奇异的程度就会比接近奇异的程度小得多。考虑到变量的量纲问题,
先要对数据标准化,标准化后的设计矩阵仍用X表示,定义称为的岭回归估计,其中,
k称为岭参数。由于假设X已经标准化,所以就是自变量样本相关阵。y可以标准化也可以未标准化,
如果y也经过标准化,那么计算的实际是标准化岭回归估计。![]() (k)作为β的估计应比最小二乘估计
(k)作为β的估计应比最小二乘估计![]() 稳定,当k=0时的岭回归估计就是普通的最小二乘估计.
稳定,当k=0时的岭回归估计就是普通的最小二乘估计.
因为岭参数k不是唯一确定的,所以得到的岭回归估计实际是回归参数的一个估计族。
则岭回归的参数估计为

python中岭回归的代码:
主要使用python中的 scikit-learn 模块
# 岭回归(Ridge 回归) from sklearn import linear_model X = [[0, 0], [1, 1], [2, 2]] y = [0, 1, 2] clf = linear_model.Ridge(alpha=0.1) # 设置k值 clf.fit(X, y) # 参数拟合 print(clf.coef_) # 系数 print(clf.intercept_) # 常量 print(clf.predict([[3, 3]])) # 求预测值 print(clf.decision_function(X)) # 求预测,等同predict print(clf.score(X, y)) # R^2,拟合优度 print(clf.get_params()) # 获取参数信息 print(clf.set_params(fit_intercept=False)) # 重新设置参数
后期的详细分析应用可以自己看linear_model的用法