理解一个数据结构,我们应该首先明白该数据结构的作用与应用场景,尔后理清其逻辑结构,基于逻辑结构考虑如何在计算机上进行物理存储,最后对以上进行代码实现。
我们按上述思考顺序来实现一次线段树。
作用及应用场景
我们考虑一个场景,我们有一个长度为 n 的数组,我们需要经常进行两种操作:
1. 计算某个区间内数组元素的和。
2. 修改数组中的某个元素。
我们考虑时间复杂度,明显的,计算区间和的时间复杂度为 O(N) ,而对于一个数组来说,修改一个元素的时间复杂度为 O(1) 。
我们想要优化一下计算区间和的时间复杂度,我们想到了生成一个新数组 sum_array ,数组下标为 n 的元素为原数组下标 0-n 的元素的元素和。如此一来,我们计算区间和的时间复杂度便优化为了 O(1) ,比如我们想要计算 i-j 的区间和,则可以直接通过 sum_array[ j ] - sum_array[ i ] 来获得,用空间换时间。
但如此一来,我们更新一个元素的时间复杂度却成了 O(n) ,因为我们如果要更新下标为 n 的元素,我们必须将 sum_array 中下标大于 n 的元素全部更新。
一个操作时间复杂度降低的代价是另一个操作时间复杂度的增加,总体效率似乎并没有提高。
线段树在该场景下应需而生,使用线段树,两种操作的时间复杂度均落在了 O(log2N) ,使总体的效率大幅提升。
逻辑结构
在优化线性结构的查询性能时我们总能想到将线性结构转化为树结构,线段树便是一棵二叉搜索树。与普通二叉树不同的是,线段树的节点值存储的是原数组的区间和。也就是说,我们将原数组的区间和转化为了一棵二叉搜索树。
比如对于一个长度为 10 的数组 arr ,我们为其构建一棵线段树。那么根节点是 arr[0] - arr[9] 的和,其左子节点为 arr[0] - arr[4] 的和,其右子节点为 arr[5] - arr[9] 的和,以此类推。若某个节点存储了原数组第 B 个节点到第 E 个节点的和,则其左子节点存储的为 B 节点到 (B+E)/2 节点的和,右子节点存储的为 (B+E)/2 + 1 节点到 E 节点的和。每个节点的值都等于其左右子节点的值的和。整棵树的结构如下图所示:
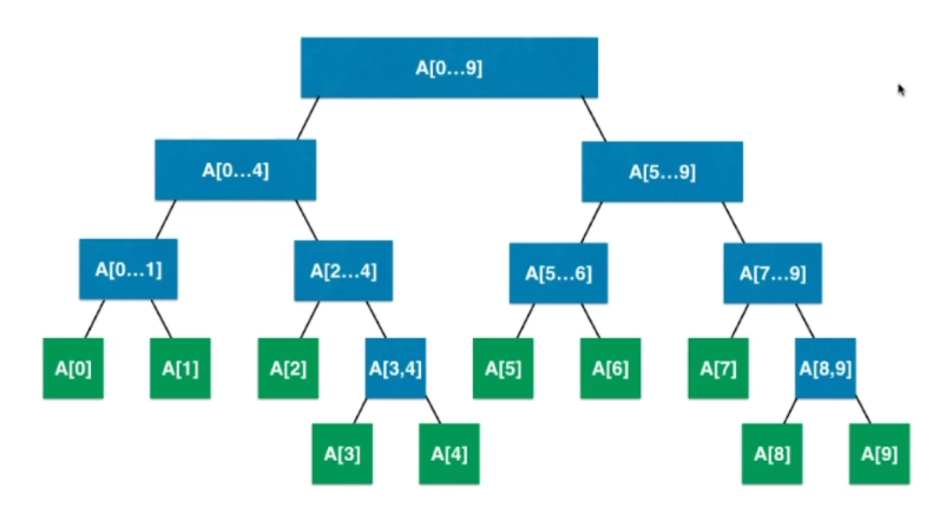
这样我们在搜索 n-m 的区间和时,只需要沿着线段树根节点向下搜索,将落在 n-m 区间内的节点的值全部返回求和即可。空间换时间,将对区间和的计算转化为了二分查找。
而在进行修改操作时,我们可以看叶子节点,每个叶子节点是一个单独的元素本身的值,我们顺着要修改的叶子节点一路向上修改,可以在稳定的时间复杂度内完成修改操作。
物理存储方式
但在上面的应用场景中,可以看到我们的建树操作往往针对的是一个确定的数组,而针对一个确定的数组建树时,树的层数及节点个数的范围我们时可以计算的。对于元素个数确定的树,我个人习惯使用数组表示,其使用连续的内存空间不容易造成内存碎片。但也要分情况考虑,如果源数组过大,使用连续存储空间会占用过多的连续内存,为底层的内存分配造成较大的压力,这种情况下更适合使用链式存储。
代码实现
代码是最重要的,也是最不重要的。我用 JAVA 和 JS 对以上逻辑进行了实现,并封装为了工具类,需要时可直接使用。
先来看 JAVA 的实现:
package learning; import java.util.ArrayList; import java.util.LinkedList; import java.util.function.Function; /** * @Author Nxy * @Date 2020/2/13 20:30 * @Description 线段树 */ public class SigmentTree { private int[] source; private int sourceLength; //依托数组构建树,本节点索引为x,左子节点索引为 2x+1 ,右子节点索引为 2x+2 private int[] targetTree; SigmentTree(int[] source) { if (source == null) { throw new RuntimeException("构建线段树时传入数组为null!"); } else { this.source = source; this.sourceLength = source.length; this.buildTree(0, 0, this.sourceLength - 1, 0); } } /** * @Author Nxy * @Date 2020/2/13 20:59 * @Description 构建线段树 */ public final int buildTree(int flagTree, int begin, int end, int depth) { //边界条件 if (begin == end) { //第一次到达叶子节点时,按照深度延迟构建承载线段树的数组;基于左右子树mid的划分方式,第一次到达最左叶子节点为深度最深的节点之一 if (targetTree == null) { targetTree = new int[(int) Math.pow(2, depth + 1)]; } targetTree[flagTree] = source[begin]; return targetTree[flagTree]; } //中继节点索引 int mid = (begin + end) / 2; //左子节点索引 int leftFlagTree = 2 * flagTree + 1; //右子节点索引 int rightFlagTree = 2 * flagTree + 2; int leftValue = buildTree(leftFlagTree, begin, mid, depth + 1); int rightValue = buildTree(rightFlagTree, mid + 1, end, depth + 1); targetTree[flagTree] = leftValue + rightValue; return targetTree[flagTree]; } /** * @Author Nxy * @Date 2020/2/13 20:55 * @Description 线段树修改元素 */ public final void update(int target, int value, int begin, int end, int treeFlag) { if (begin == end) { if (begin != target) { throw new RuntimeException("待修改元素下表不在数组内!"); } targetTree[treeFlag] = value; source[target] = value; return; } int mid = (begin + end) / 2; int leftFlagTree = treeFlag * 2 + 1; int rightFlagTree = treeFlag * 2 + 2; if (target <= mid) { update(target, value, begin, mid, leftFlagTree); } else { update(target, value, mid + 1, end, rightFlagTree); } targetTree[treeFlag] = targetTree[leftFlagTree] + targetTree[rightFlagTree]; } /** * @Author Nxy * @Date 2020/2/13 20:47 * @Description 查询区间和, 沿着线段树一路向下搜索,查询范围内的节点值返回,否则略过 */ public final int qurey(int begin, int end, int nodeBegin, int nodeEnd, int treeFlag) { //到达叶子节点 if ((nodeBegin == nodeEnd) && nodeBegin >= begin && nodeEnd <= end) { return targetTree[treeFlag]; } //整个节点都在查询区间内,直接返回 if (begin <= nodeBegin && end >= nodeEnd) { return targetTree[treeFlag]; } int mid = (nodeBegin + nodeEnd) / 2; int leftTargetTree = treeFlag * 2 + 1; int rightTargetTree = treeFlag * 2 + 2; if (end <= mid) { //搜索区间整个落在左子节点 return qurey(begin, end, nodeBegin, mid, leftTargetTree); } else if (begin > mid) { //搜索区间整个落在右子节点 return qurey(begin, end, mid + 1, nodeEnd, rightTargetTree); } else { //搜索区间横跨左右子节点 return qurey(begin, end, nodeBegin, mid, leftTargetTree) + qurey(begin, end, mid + 1, nodeEnd, rightTargetTree); } } /** * @Author Nxy * @Date 2020/2/13 20:59 * @Description 打印数组 */ private final void printArr(int[] arr) { if (arr == null) { throw new NullPointerException("input num is null"); } int length = arr.length; for (int i = 0; i < length; i++) { System.out.print(arr[i] + " , "); } System.out.print(System.lineSeparator()); } }
所有属性都是 private 的,而且没有提供 getter 和 setter,因为线段树与原数组是一一对应的,不能允许使用者单独修改其中任何一个数组,否则会造成逻辑错误。我们只允许通过 update方法修改数组中的元素值。
使用非常简单:
public static void main(String[] args) { int[] arr = new int[1000000]; for (int i = 0; i < 1000000; i++) { arr[i] = i; } SigmentTree st = new SigmentTree(arr); Function<int[], Integer> f = (array) -> { int an = 0; for (int i = 3333; i <= 777777; i++) { an += arr[i]; } return an; }; long now = System.currentTimeMillis(); System.out.println(f.apply(arr)); System.out.println("遍历区间查询用时 : " + String.valueOf(System.currentTimeMillis() - now)); now = System.currentTimeMillis(); System.out.println(st.qurey(3333, 777777, 0, st.sourceLength - 1, 0)); System.out.println("线段树区间查询用时 : " + String.valueOf(System.currentTimeMillis() - now)); int[] source = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; st=new SigmentTree(source); st.buildTree(0, 0, st.sourceLength - 1, 0); st.printArr(st.targetTree); st.update(0, 5, 0, st.sourceLength - 1, 0); st.printArr(st.targetTree); System.out.println("4-6:" + st.qurey(3, 5, 0, st.sourceLength - 1, 0)); System.out.println("9-10:" + st.qurey(8, 9, 0, st.sourceLength - 1, 0)); System.out.println("1-2:" + st.qurey(0, 1, 0, st.sourceLength - 1, 0)); System.out.println("2-4:" + st.qurey(1, 3, 0, st.sourceLength - 1, 0)); System.out.println("1-10:" + st.qurey(0, 9, 0, st.sourceLength - 1, 0)); System.out.println("1-9:" + st.qurey(0, 8, 0, st.sourceLength - 1, 0)); }
我们看下执行结果:

对于长度为 10W 的数组,可以看出区间查询用时的差距非常大(单位为 ms )。其余结果用于验证方法的正确性。
下面看 JS 的实现:
<!--线段树构建方法开始-->
//线段树原型对象
var sigmentTreePrototype={
//构建线段树方法,存在函数副作用,改变调用对象中的 sigment_tree 属性将其初始化为线段树
build:function(begin_node,end_node,flag_tree,depth){
if(begin_node==end_node){
if("undefined"==typeof(this.sigment_tree)){
//确定树的大小后延迟创建树
var length_array=Math.pow(2,depth)-1;
//console.log("build new tree and length_array is : "+length_array+" typeof tree is : "+typeof(this.sigment_tree) );
this.sigment_tree=new Array(length_array).fill(0);
}
this.sigment_tree[flag_tree]=this.source_array[begin_node];
return;
}
var mid=parseInt((begin_node+end_node)/2);
var left_tree=flag_tree*2+1;
var right_tree=flag_tree*2+2;
this.build(begin_node,mid,left_tree,depth+1);
this.build(mid+1,end_node,right_tree,depth+1);
this.sigment_tree[flag_tree]=this.sigment_tree[left_tree]+this.sigment_tree[right_tree];
},
//修改原数组中的某个值,更新树
update:function(begin_node,end_node,flag_tree,target_array,target_value){
if(begin_node==end_node){
this.source_array[target_array]=target_value;
this.sigment_tree[flag_tree]=target_value;
return target_value;
}
var mid=parseInt((begin_node+end_node)/2);
var left_tree=flag_tree*2+1;
var right_tree=flag_tree*2+2;
if(target_array<=mid){
this.update(begin_node,mid,left_tree,target_array,target_value);
}else{
this.update(mid+1,end_node,right_tree,target_array,target_value);
}
this.sigment_tree[flag_tree]=this.sigment_tree[left_tree]+this.sigment_tree[right_tree];
},
//查找区间和
qurey:function(begin_node,end_node,flag_tree,begin_search,end_search){
if(begin_node==end_node){
if(begin_node>=begin_search&&end_node<=end_search){
return this.sigment_tree[flag_tree];
}else{
return 0;
}
}
if(begin_node>=begin_search&&end_node<=end_search){
return this.sigment_tree[flag_tree];
}
var mid=parseInt((begin_node+end_node)/2);
var left_tree=flag_tree*2+1;
var right_tree=flag_tree*2+2;
if(begin_search>mid){
return this.qurey(mid+1,end_node,right_tree,begin_search,end_search);
}else if(end_search<=mid){
return this.qurey(begin_node,mid,left_tree,begin_search,end_search);
}else{
return this.qurey(mid+1,end_node,right_tree,begin_search,end_search)+this.qurey(begin_node,mid,left_tree,begin_search,end_search);
}
}
}
//线段树构造方法
function SigmentTree(arr){
if(!arr.constructor===Array){
throw new Error("arr is not Array!");
}
this.source_array=arr;
this.length_array=arr.length;
this.sigment_tree=undefined;
this.build(0,this.length_array-1,0,1);
}
//初始化原型链
SigmentTree.prototype=sigmentTreePrototype;
sigmentTreePrototype.constructor=SigmentTree;
<!--线段树构建方法结束-->
使用起来非常简单:
var array=[1,2,3,4,5,6,7,8,9,10];
//获取 array 的线段树
var array_sigmentTree=new SigmentTree(array);
console.log(array_sigmentTree.sigment_tree);
//将第 0 个元素更新为 5
array_sigmentTree.update(0,array_sigmentTree.length_array-1,0,0,5);
console.log(array_sigmentTree.sigment_tree);
//将第 0 个元素恢复为 0
array_sigmentTree.update(0,array_sigmentTree.length_array-1,0,0,1);
//计算区间和
console.log("区间和 1-10 : "+array_sigmentTree.qurey(0,array_sigmentTree.length_array-1,0,0,9));
console.log("区间和 2-3 : "+array_sigmentTree.qurey(0,array_sigmentTree.length_array-1,0,1,2));
console.log("区间和 6-9 : "+array_sigmentTree.qurey(0,array_sigmentTree.length_array-1,0,5,8));
console.log("区间和 2-7 : "+array_sigmentTree.qurey(0,array_sigmentTree.length_array-1,0,1,6));
//释放引用,方便 GC
array_sigmentTree=null;
我们看下执行结果:

最近找到了一款非常舒服的配色: