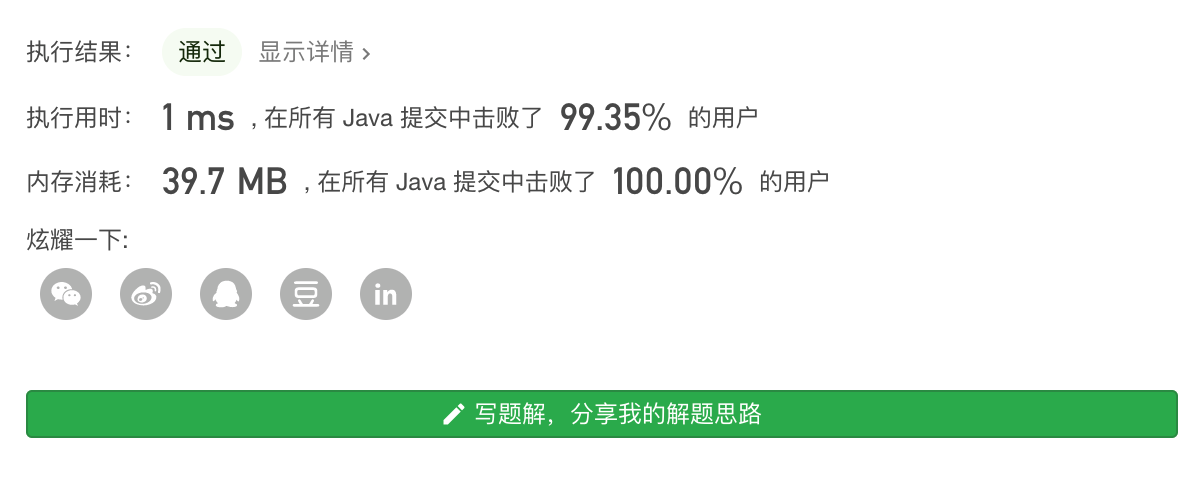
比较常规的解法为回溯解法:
List<List<Integer>> reList = new LinkedList<List<Integer>>(); public final List<List<Integer>> subsets1(int[] nums) { reList.add(new ArrayList<Integer>()); Stack<Integer> stack = new Stack<Integer>(); //所有可能长度 for (int i = 1; i <= nums.length; i++) { //所有可能头元素 for (int j = 0; j <= nums.length - i; j++) { subWay(nums, j, i, stack); } } return reList; } /** * @Author Niuxy * @Date 2020/7/21 12:26 下午 * @Description 遍历已 flag 为头元素,长度为 length 的所有可能子序列 */ private final void subWay(int[] nums, int flag, int length, Stack<Integer> stack) { if (length == 1) { if (flag < nums.length) { stack.push(nums[flag]); reList.add(new ArrayList<Integer>(stack)); stack.pop(); } return; } if (length > nums.length - flag || flag > nums.length) { return; } stack.push(nums[flag]); for (int i = flag + 1; i < nums.length; i++) { subWay(nums, i, length - 1, stack); } stack.pop(); }
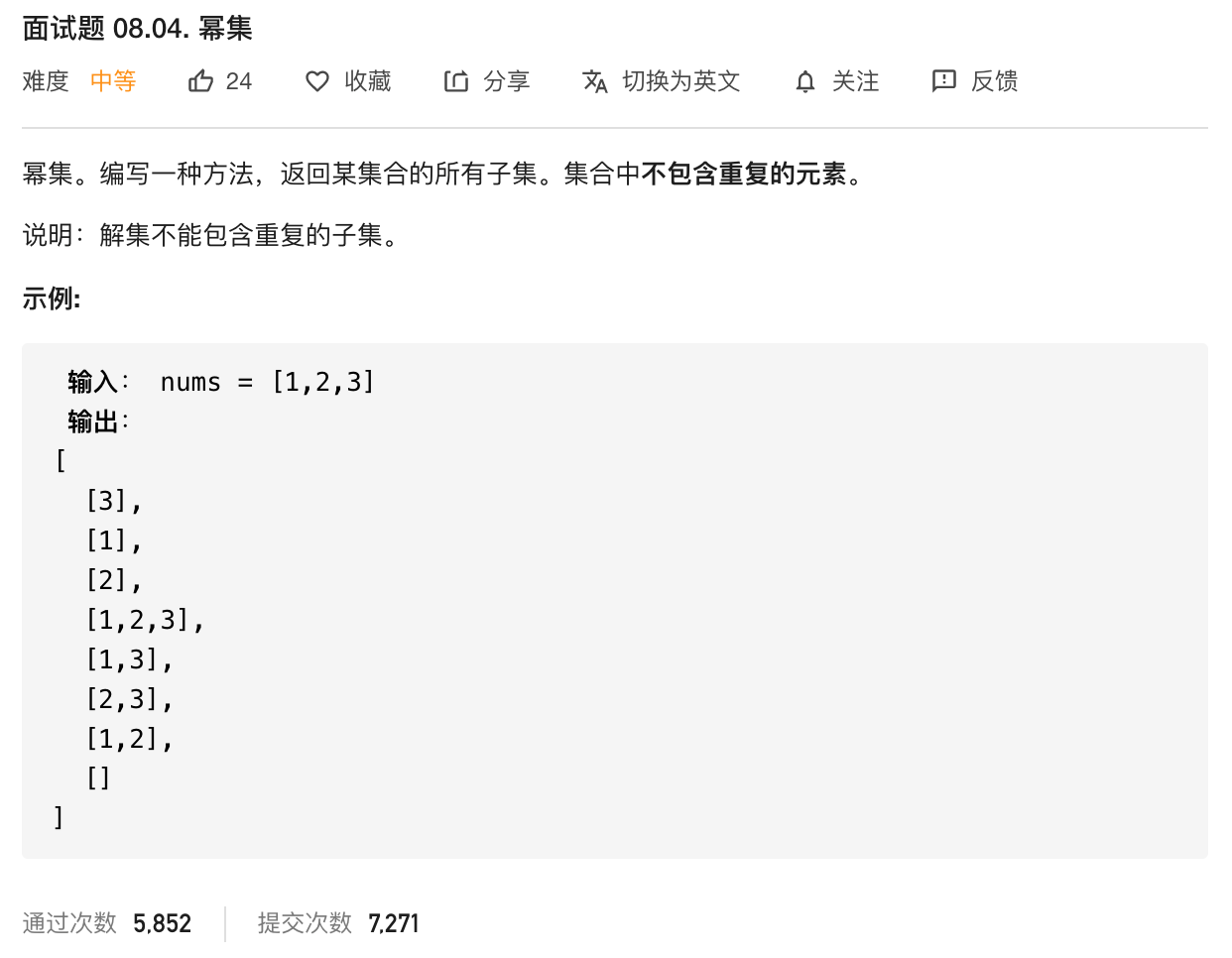
除此之外还有一种取巧的方法:位图。
每个自然数都是独一无二的,它们的二进制表示形式也是。
对于 n 个元素的输入,将会有 二的 N 次方(设为 k )种排列组合方式。
0 的二进制表示为 00000000 000000000 00000000 00000000
1 的二进制表示为 00000000 000000000 00000000 00000001
2 的二进制表示为 00000000 00000000 00000000 00000010
对于每个数的二进制表示,对应到输入的数组下标,1 表示选择该元素,0 表示不选择该元素。
则从 1 到 k 的位图可以完全的表示所有可能的组合。
位图解法:
/** * @Author Niuxy * @Date 2020/7/21 12:31 下午 * @Description 位图解法 */ public final List<List<Integer>> subsets(int[] nums) { int source = (int) Math.pow(2, nums.length); List<List<Integer>> reList = new LinkedList<List<Integer>>(); for (int i = 1; i <= source; i++) { List<Integer> inList = new LinkedList<Integer>(); for (int j = 0; j < nums.length; j++) { if (((i >>> j) & 1) == 1) { inList.add(nums[j]); } } reList.add(inList); } return reList; }
位图解法效果: