zoukankan      html  css  js  c++  java

  • CodeForces 438D 线段树 剪枝

    D. The Child and Sequence
    time limit per test
    4 seconds
    memory limit per test
    256 megabytes
    input
    standard input
    output
    standard output

    At the children's day, the child came to Picks's house, and messed his house up. Picks was angry at him. A lot of important things were lost, in particular the favorite sequence of Picks.

    Fortunately, Picks remembers how to repair the sequence. Initially he should create an integer array a[1], a[2], ..., a[n]. Then he should perform a sequence of m operations. An operation can be one of the following:

    1. Print operation l, r. Picks should write down the value of .
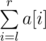    2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for each i (l ≤ i ≤ r).
    3. Set operation k, x. Picks should set the value of a[k] to x (in other words perform an assignment a[k] = x).

    Can you help Picks to perform the whole sequence of operations?

    Input

    The first line of input contains two integer: n, m (1 ≤ n, m ≤ 105). The second line contains n integers, separated by space: a[1], a[2], ..., a[n] (1 ≤ a[i] ≤ 109) — initial value of array elements.

    Each of the next m lines begins with a number type .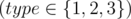

    • If type = 1, there will be two integers more in the line: l, r (1 ≤ l ≤ r ≤ n), which correspond the operation 1.
    • If type = 2, there will be three integers more in the line: l, r, x (1 ≤ l ≤ r ≤ n; 1 ≤ x ≤ 109), which correspond the operation 2.
    • If type = 3, there will be two integers more in the line: k, x (1 ≤ k ≤ n; 1 ≤ x ≤ 109), which correspond the operation 3.
    Output

    For each operation 1, please print a line containing the answer. Notice that the answer may exceed the 32-bit integer.

    Sample test(s)
    Input
    5 5 1 2 3 4 5 2 3 5 4 3 3 5 1 2 5 2 1 3 3 1 1 3
    Output
    8 5
    Input
    10 10 6 9 6 7 6 1 10 10 9 5 1 3 9 2 7 10 9 2 5 10 8 1 4 7 3 3 7 2 7 9 9 1 2 4 1 6 6 1 5 9 3 1 10
    Output
    49 15 23 1 9
    Note

    Consider the first testcase:

    • At first, a = {1, 2, 3, 4, 5}.
    • After operation 1, a = {1, 2, 3, 0, 1}.
    • After operation 2, a = {1, 2, 5, 0, 1}.
    • At operation 3, 2 + 5 + 0 + 1 = 8.
    • After operation 4, a = {1, 2, 2, 0, 1}.
    • At operation 5, 1 + 2 + 2 = 5.

    注意：剪枝：若x<mod,x=x;

      1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdlib>
  4 #include<cstdio>
  5 #include<algorithm>
  6 #include<cmath>
  7 #include<queue>
  8 #include<map>
  9 
 10 #define N 100010
 11 #define M 15
 12 //#define mod 1000000007
 13 //#define mod2 100000000
 14 #define ll long long
 15 #define maxi(a,b) (a)>(b)? (a) : (b)
 16 #define mini(a,b) (a)<(b)? (a) : (b)
 17 
 18 using namespace std;
 19 
 20 int n,q;
 21 int x[N];
 22 int type;
 23 int a,b,c;
 24 
 25 struct node
 26 {
 27     ll sum;
 28     int ma;
 29 }tree[4*N];
 30 /*
 31 void update(int l,int r,int i)
 32 {
 33     if(!tree[i].mark) return;
 34     int mid=(l+r)/2;
 35     tree[2*i].sum+=tree[i].mark*(ll)(mid-l+1);
 36     tree[2*i+1].sum+=tree[i].mark*(ll)(r-mid);
 37     tree[2*i].mark+=tree[i].mark;
 38     tree[2*i+1].mark+=tree[i].mark;
 39     tree[i].mark=0;
 40 
 41 }*/
 42 
 43 ll query(int tl,int tr,int l,int r,int i)
 44 {
 45     if(tl>r || tr<l)
 46         return 0;
 47     if(tl<=l && r<=tr)
 48         return tree[i].sum;
 49    // update(l,r,i);
 50     int mid=(l+r)/2;
 51 
 52     return query(tl,tr,l,mid,2*i)+query(tl,tr,mid+1,r,2*i+1);
 53 }
 54 /*
 55 void addd(int tl,int tr,int l,int r,int i,int val)
 56 {
 57     if(tl>r || tr<l)
 58         return;
 59     if(tl<=l && tr>=r){
 60         tree[i].sum+=val*(ll)(r-l+1);
 61         tree[i].mark+=val;
 62         return;
 63     }
 64     update(l,r,i);
 65     int mid=(l+r)/2;
 66     addd(tl,tr,l,mid,2*i,val);
 67     addd(tl,tr,mid+1,r,2*i+1,val);
 68     tree[i].sum=tree[2*i].sum+tree[2*i+1].sum;
 69 }*/
 70 
 71 void modefiyMod(int tl,int tr, int l, int r,int i,int mod)
 72 {
 73     if(tree[i].ma<mod) return;
 74     if(l==r){
 75         tree[i].sum=tree[i].ma=tree[i].sum%mod;
 76         return;
 77     }
 78     else{
 79         int mid=(l+r)/2;
 80         if(tr<=mid){
 81             modefiyMod(tl,tr,l,mid,i*2,mod);
 82         }
 83         else if(tl>mid){
 84             modefiyMod(tl,tr,mid+1,r,i*2+1,mod);
 85         }
 86         else{
 87             modefiyMod(tl,tr,l,mid,i*2,mod);
 88             modefiyMod(tl,tr,mid+1,r,i*2+1,mod);
 89         }
 90         tree[i].sum=tree[2*i].sum+tree[2*i+1].sum;
 91         tree[i].ma=max(tree[2*i].ma,tree[2*i+1].ma);
 92     }
 93 }
 94 
 95 void setVal(int i, int l, int r,int x,int v)
 96 {
 97     if(l==r){
 98         tree[i].sum=tree[i].ma=v;
 99         return;
100     }
101     else{
102         int mid=(l+r)/2;
103         if(x<=mid){
104             setVal(i*2,l,mid,x,v);
105         }
106         else{
107             setVal(i*2+1,mid+1,r,x,v);
108         }
109         tree[i].sum=tree[2*i].sum+tree[2*i+1].sum;
110         tree[i].ma=max(tree[2*i].ma,tree[2*i+1].ma);
111     }
112 }
113 
114 void build_tree(int l,int r,int i)
115 {
116     if(l==r){
117         tree[i].sum=x[l];
118         tree[i].ma=x[l];
119         return;
120     }
121     int mid=(l+r)/2;
122     build_tree(l,mid,2*i);
123     build_tree(mid+1,r,2*i+1);
124     tree[i].sum=tree[2*i].sum+tree[2*i+1].sum;
125     tree[i].ma=max(tree[2*i].ma,tree[2*i+1].ma);
126 }
127 
128 int main()
129 {
130     int i;
131     //freopen("data.in","r",stdin);
132     //scanf("%d",&T);
133     //for(int cnt=1;cnt<=T;cnt++)
134     //while(T--)
135     while(scanf("%d%d",&n,&q)!=EOF)
136     {
137        for(i=1;i<=n;i++) scanf("%d",&x[i]);
138        memset(tree,0,sizeof(tree));
139        build_tree(1,n,1);
140        while(q--){
141             scanf("%d",&type);
142             if(type==1){
143                 scanf("%d%d",&a,&b);
144                 ll ans=query(a,b,1,n,1);
145                 printf("%I64d
",ans);
146 
147             }
148             else if(type==2){
149                 scanf("%d%d%d",&a,&b,&c);
150                 modefiyMod(a, b, 1, n, 1, c);
151             }
152             else{
153                 scanf("%d%d",&a,&b);
154                 setVal(1, 1, n, a, b);
155             }
156        }
157     }
158 
159     return 0;
160 }
  • 相关阅读:
    Shell脚本中循环语句for,while,until用法
    国内yum源的安装(163，阿里云，epel)
    express高效入门教程（4）
    express高效入门教程（3）
    express高效入门教程（2）
    express高效入门教程（1）
    dart快速入门教程 （8）
    dart快速入门教程 （7.4）
    dart快速入门教程 （7.3）
    dart快速入门教程 （7.2）
  • 原文地址：https://www.cnblogs.com/njczy2010/p/3920227.html
Copyright © 2011-2022 走看看