Bayan 2015 Contest Warm Up D. CGCDSSQ （math，pair，map，暴力）

哎，只能转题解了，，，

8165031	2014-10-10 15:53:42	njczy2010	D - CGCDSSQ	GNU C++	Accepted	156 ms	27584 KB
8163765	2014-10-10 13:03:56	njczy2010	D - CGCDSSQ	GNU C++	Time limit exceeded on test 10	2000 ms	32600 KB
8163761	2014-10-10 13:02:38	njczy2010	D - CGCDSSQ	GNU C++	Time limit exceeded on test 10	2000 ms	31600 KB
8163755	2014-10-10 13:01:12	njczy2010	D - CGCDSSQ	GNU C++	Wrong answer on test 9	46 ms	19700 KB
8163749	2014-10-10 12:59:54	njczy2010	D - CGCDSSQ	GNU C++	Wrong answer on test 9	31 ms	2100 KB

D. CGCDSSQ

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given a sequence of integers a₁, ..., a_n and q queries x₁, ..., x_q on it. For each query x_i you have to count the number of pairs (l, r) such that 1 ≤ l ≤ r ≤ n and gcd(a_l, a_l + 1, ..., a_r) = x_i.

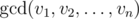is a greatest common divisor of v₁, v₂, ..., v_n, that is equal to a largest positive integer that divides all v_i.

Input

The first line of the input contains integer n, (1 ≤ n ≤ 10⁵), denoting the length of the sequence. The next line contains n space separated integers a₁, ..., a_n, (1 ≤ a_i ≤ 10⁹).

The third line of the input contains integer q, (1 ≤ q ≤ 3 × 10⁵), denoting the number of queries. Then follows q lines, each contain an integer x_i, (1 ≤ x_i ≤ 10⁹).

Output

For each query print the result in a separate line.

Sample test(s)

Input

3 2 6 3 5 1 2 3 4 6

Output

1 2 2 0 1

Input

7 10 20 3 15 1000 60 16 10 1 2 3 4 5 6 10 20 60 1000

Output

14 0 2 2 2 0 2 2 1 1

题解以代码转自：http://blog.csdn.net/accelerator_/article/details/39892385

D：记录下gcd，每次多一个数字，就和前面的数字都取gcd，然后合并掉，下次利用这些已有的gcd去做，然后合并的过程要利用到gcd的递减性质，就可以直接从头往后找即可

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<string>
//#include<pair>

#define N 1000005
#define M 1000005
#define mod 1000000007
//#define p 10000007
#define mod2 100000000
#define ll long long
#define LL long long
#define maxi(a,b) (a)>(b)? (a) : (b)
#define mini(a,b) (a)<(b)? (a) : (b)

using namespace std;

int n,q;
int a[N];
map<int,ll>ans;
typedef pair<int,ll>PP;
PP save[N];
int tot;

int gcd(int x,int y)
{
    if(y==0)
        return x;
    return gcd(y,x%y);
}

void ini()
{
    int i;
    ans.clear();
    tot=0;
    for(i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
}

void solve()
{
    int i,j;
    int sn;
    for(i=1;i<=n;i++){
        for(j=0;j<tot;j++){
            save[j].first=gcd(save[j].first,a[i]);
        }
        save[tot]=make_pair(a[i],1);
        tot++;
        sn=0;
        for(j=1;j<tot;j++){
            if(save[sn].first==save[j].first){
                save[sn].second+=save[j].second;
            }
            else{
                sn++;
                save[sn]=save[j];
            }
        }
        sn++;
        tot=sn;
        for(j=0;j<tot;j++){
            ans[ save[j].first ]+=save[j].second;
        }
    }
}

void out()
{
    int x;
    scanf("%d",&q);
    while(q--){
        scanf("%d",&x);
        printf("%I64d
",ans[x]);
    }
}

int main()
{
    //freopen("data.in","r",stdin);
    //freopen("data.out","w",stdout);
   // scanf("%d",&T);
   // for(int ccnt=1;ccnt<=T;ccnt++)
   // while(T--)
    while(scanf("%d",&n)!=EOF)
    {
        //if(n==0 && k==0 ) break;
        //printf("Case %d: ",ccnt);
        ini();
        solve();
        out();
    }

    return 0;
}