Codeforces Round #278 (Div. 2) B. Candy Boxes [brute force+constructive algorithms]

哎，最近弱爆了，，，不过这题还是不错滴~~ 要考虑完整各种情况

8795058	2014-11-22 06:52:58	njczy2010	B - Candy Boxes	GNU C++	Accepted	31 ms	4 KB
8795016	2014-11-22 06:48:15	njczy2010	B - Candy Boxes	GNU C++	Wrong answer on test 13	30 ms	0 KB
8795000	2014-11-22 06:44:39	njczy2010	B - Candy Boxes	GNU C++	Wrong answer on test 5	15 ms	0 KB

B. Candy Boxes

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There is an old tradition of keeping 4 boxes of candies in the house in Cyberland. The numbers of candies are special if their arithmetic mean, their median and their range are all equal. By definition, for a set {x₁, x₂, x₃, x₄} (x₁ ≤ x₂ ≤ x₃ ≤ x₄) arithmetic mean is , median is 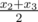and range is x₄ - x₁. The arithmetic mean and median are not necessary integer. It is well-known that if those three numbers are same, boxes will create a "debugging field" and codes in the field will have no bugs.

For example, 1, 1, 3, 3 is the example of 4 numbers meeting the condition because their mean, median and range are all equal to 2.

Jeff has 4 special boxes of candies. However, something bad has happened! Some of the boxes could have been lost and now there are only n (0 ≤ n ≤ 4) boxes remaining. The i-th remaining box contains a_i candies.

Now Jeff wants to know: is there a possible way to find the number of candies of the 4 - n missing boxes, meeting the condition above (the mean, median and range are equal)?

Input

The first line of input contains an only integer n (0 ≤ n ≤ 4).

The next n lines contain integers a_i, denoting the number of candies in the i-th box (1 ≤ a_i ≤ 500).

Output

In the first output line, print "YES" if a solution exists, or print "NO" if there is no solution.

If a solution exists, you should output 4 - n more lines, each line containing an integer b, denoting the number of candies in a missing box.

All your numbers b must satisfy inequality 1 ≤ b ≤ 10⁶. It is guaranteed that if there exists a positive integer solution, you can always find such b's meeting the condition. If there are multiple answers, you are allowed to print any of them.

Given numbers a_i may follow in any order in the input, not necessary in non-decreasing.

a_i may have stood at any positions in the original set, not necessary on lowest n first positions.

Sample test(s)

Input

2 1 1

Output

YES 3 3

Input

3 1 1 1

Output

NO

Input

4 1 2 2 3

Output

YES

Note

For the first sample, the numbers of candies in 4 boxes can be 1, 1, 3, 3. The arithmetic mean, the median and the range of them are all 2.

For the second sample, it's impossible to find the missing number of candies.

In the third example no box has been lost and numbers satisfy the condition.

You may output b in any order.

主要就是根据那三个等式，化简，得两个方程：

x4=3*x1;

x2+x3=4*x1;

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<string>
//#include<pair>

#define N 10005
#define M 1005
#define mod 1000000007
//#define p 10000007
#define mod2 1000000000
#define ll long long
#define LL long long
#define eps 1e-9
#define maxi(a,b) (a)>(b)? (a) : (b)
#define mini(a,b) (a)<(b)? (a) : (b)

using namespace std;

int n;
int a[10];
int b[10];
int flag;

void ini()
{
    flag=0;
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
    sort(a+1,a+1+n);
}

void solve0()
{
    flag=1;
    b[1]=1;b[2]=1;b[3]=3;b[4]=3;
}

void solve1()
{
    flag=1;
    b[1]=a[1];b[2]=3*a[1];b[3]=3*a[1];
}

void solve2()
{
    if(a[2]%3==0){
        if(a[2]/3==a[1]){
            flag=1;
            b[1]=a[1];b[2]=a[2];
        }
        else if(a[2]/3<a[1]){
            flag=1;b[1]=a[2]/3;b[2]=a[2]+b[1]-a[1];
        }
        else{
            return;
        }
    }
    else{
        if(a[1]*3<=a[2]){
            return;
        }
        else{
            flag=1;
            b[2]=a[1]*3;
            b[1]=b[2]+a[1]-a[2];
        }
    }
}

void solve3()
{
    if(a[3]%3!=0){
        if(a[1]*3<=a[3]){
            return;
        }
        else{
            if(a[1]*4==a[2]+a[3]){
                flag=1;b[1]=a[1]*3;
            }
            else return;
        }
    }
    else{
        if(a[3]/3==a[1]){
            flag=1;
            b[1]=a[1]+a[3]-a[2];
        }
        else if(a[3]/3<a[1]){
            b[1]=a[3]/3;
            if(b[1]+a[3]==a[1]+a[2]){
                flag=1;
            }
            else return;
        }
        else{
            return;
        }
    }
}

void solve4()
{
    if(a[4]==3*a[1] && a[2]+a[3]==4*a[1]){
        flag=1;
    }
}

void solve()
{
    if(n==4){
        solve4();
    }
    else if(n==0){
        solve0();
    }
    else if(n==1){
        solve1();
    }
    else if(n==2){
        solve2();
    }
    else if(n==3){
        solve3();
    }
}

void out()
{
    int i;
    if(flag==1){
        printf("YES
");
        for(i=1;i<=4-n;i++){
            printf("%d
",b[i]);
        }
    }
    else{
        printf("NO
");
    }
}

int main()
{
    //freopen("data.in","r",stdin);
    //freopen("data.out","w",stdout);
    //scanf("%d",&T);
    //for(int ccnt=1;ccnt<=T;ccnt++)
   // while(T--)
    while(scanf("%d",&n)!=EOF)
    {
       // if(n==0 && m==0 ) break;
        //printf("Case %d: ",ccnt);
        ini();
        solve();
        out();
    }

    return 0;
}