zoukankan      html  css  js  c++  java

  • Codeforces Round #287 (Div. 2) E. Breaking Good [Dijkstra 最短路 优先队列]

    传送门

    E. Breaking Good
    time limit per test
    2 seconds
    memory limit per test
    256 megabytes
    input
    standard input
    output
    standard output

    Breaking Good is a new video game which a lot of gamers want to have. There is a certain level in the game that is really difficult even for experienced gamers.

    Walter William, the main character of the game, wants to join a gang called Los Hermanos (The Brothers). The gang controls the whole country which consists of n cities with m bidirectional roads connecting them. There is no road is connecting a city to itself and for any two cities there is at most one road between them. The country is connected, in the other words, it is possible to reach any city from any other city using the given roads.

    The roads aren't all working. There are some roads which need some more work to be performed to be completely functioning.

    The gang is going to rob a bank! The bank is located in city 1. As usual, the hardest part is to escape to their headquarters where the police can't get them. The gang's headquarters is in city n. To gain the gang's trust, Walter is in charge of this operation, so he came up with a smart plan.

    First of all the path which they are going to use on their way back from city 1 to their headquarters n must be as short as possible, since it is important to finish operation as fast as possible.

    Then, gang has to blow up all other roads in country that don't lay on this path, in order to prevent any police reinforcements. In case of non-working road, they don't have to blow up it as it is already malfunctional.

    If the chosen path has some roads that doesn't work they'll have to repair those roads before the operation.

    Walter discovered that there was a lot of paths that satisfied the condition of being shortest possible so he decided to choose among them a path that minimizes the total number of affected roads (both roads that have to be blown up and roads to be repaired).

    Can you help Walter complete his task and gain the gang's trust?

    Input

    The first line of input contains two integers n, m (2 ≤ n ≤ 105, 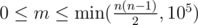), the number of cities and number of roads respectively.

    In following m lines there are descriptions of roads. Each description consists of three integers x, y, z (1 ≤ x, y ≤ n, 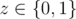) meaning that there is a road connecting cities number x and y. If z = 1, this road is working, otherwise it is not.

    Output

    In the first line output one integer k, the minimum possible number of roads affected by gang.

    In the following k lines output three integers describing roads that should be affected. Each line should contain three integers x, y, z (1 ≤ x, y ≤ n, 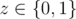), cities connected by a road and the new state of a road. z = 1 indicates that the road between cities x and y should be repaired and z = 0 means that road should be blown up.

    You may output roads in any order. Each affected road should appear exactly once. You may output cities connected by a single road in any order. If you output a road, it's original state should be different from z.

    After performing all operations accroding to your plan, there should remain working only roads lying on some certain shortest past between city 1 and n.

    If there are multiple optimal answers output any.

    Sample test(s)
    Input
    2 1
    1 2 0
    Output
    1
    1 2 1
    Input
    4 4
    1 2 1
    1 3 0
    2 3 1
    3 4 1
    Output
    3
    1 2 0
    1 3 1
    2 3 0
    Input
    8 9
    1 2 0
    8 3 0
    2 3 1
    1 4 1
    8 7 0
    1 5 1
    4 6 1
    5 7 0
    6 8 0
    Output
    3
    2 3 0
    1 5 0
    6 8 1
    Note

    In the first test the only path is 1 - 2

    In the second test the only shortest path is 1 - 3 - 4

    In the third test there are multiple shortest paths but the optimal is 1 - 4 - 6 - 8

    有n个城市，m条边。让你求出来1到n的最短路，但是要求，保证最短路的时候，要求权值最大。

    最开始没反应过来是求最短路问题，直接bfs，，，跪惨。。。。

    一开始我试图在结构体里面用个string类型的变量来记录路径，但是wa了，不懂为什么。
    现在好像懂了，，，编号太大，，，爆char了，，，，果然string记录路径就是个坑，，，
     
    9557892 2015-01-26 11:37:48 njczy2010 E - Breaking Good GNU C++ Accepted 124 ms 19100 KB
    9557655 2015-01-26 11:12:44 njczy2010 E - Breaking Good GNU C++ Accepted 623 ms 19300 KB
    9557440 2015-01-26 10:51:36 njczy2010 E - Breaking Good GNU C++ Wrong answer on test 8 31 ms 6100 KB
    9557233 2015-01-26 10:29:53 njczy2010 E - Breaking Good GNU C++ Wrong answer on test 8 15 ms 6200 KB 
      1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdlib>
  4 #include<cstdio>
  5 #include<algorithm>
  6 #include<cmath>
  7 #include<queue>
  8 #include<map>
  9 #include<set>
 10 #include<stack>
 11 #include<string>
 12 
 13 #define N 100005
 14 #define M 105
 15 #define mod 1000000007
 16 //#define p 10000007
 17 #define mod2 1000000000
 18 #define ll long long
 19 #define LL long long
 20 #define eps 1e-6
 21 #define inf 100000000
 22 #define maxi(a,b) (a)>(b)? (a) : (b)
 23 #define mini(a,b) (a)<(b)? (a) : (b)
 24 
 25 using namespace std;
 26 
 27 int n,m;
 28 int x[N],y[N],z[N];
 29 int tot;
 30 
 31 typedef struct
 32 {
 33     int a,b;
 34     int f;
 35 }AA;
 36 
 37 AA ans[N];
 38 
 39 typedef struct
 40 {
 41     int to;
 42     int f;
 43     int indexb;
 44 }PP;
 45 
 46 vector<PP>bian[N];
 47 int vis[N];
 48 int Step[N];
 49 int Cnt[N];
 50 
 51 struct QQ
 52 {
 53     friend bool operator < (QQ n1,QQ n2)
 54     {
 55         if(n1.step==n2.step){
 56             return n1.cnt>n2.cnt;
 57         }
 58         else{
 59             return n1.step>n2.step;
 60         }
 61     }
 62     int index;
 63     int cnt;
 64     int indexn;
 65     int pre;
 66     int step;
 67 };
 68 
 69 void out(QQ te);
 70 
 71 void ini()
 72 {
 73     int i;
 74     tot=0;
 75     memset(vis,0,sizeof(vis));
 76     PP te;
 77     for(i=1;i<=n;i++){
 78         bian[i].clear();
 79         Step[i]=inf;
 80         Cnt[i]=inf;
 81     }
 82     Step[1]=0;
 83     Cnt[1]=0;
 84     for(i=1;i<=m;i++){
 85         scanf("%d%d%d",&x[i],&y[i],&z[i]);
 86         te.to=y[i];te.f=z[i];te.indexb=i;
 87         bian[ x[i] ].push_back(te);
 88         te.to=x[i];
 89         bian[ y[i] ].push_back(te);
 90     }
 91 }
 92 
 93 typedef struct
 94 {
 95     int in;
 96     int pre;
 97 }NN;
 98 
 99 NN node[N*10];
100 int totnode;
101 
102 void bfs()
103 {
104     priority_queue <QQ>q;
105     QQ te,nt;
106     te.index=1;
107     te.cnt=0;
108     te.step=0;
109     totnode=0;
110     te.indexn=-1;
111     te.pre=-1;
112     q.push(te);
113     int st;
114     PP yy;
115     vector<PP>::iterator it;
116     while(q.size()>=1)
117     {
118         te=q.top();
119         q.pop();
120         if(te.index==n){
121             out(te);
122             return;
123         }
124         if(vis[te.index]==1) continue;
125         vis[te.index]=1;
126         st=te.index;
127         for(it=bian[st].begin();it!=bian[st].end();it++)
128         {
129             yy=*it;
130             if(vis[yy.to]==1) continue;
131             nt.index=yy.to;
132             nt.cnt=te.cnt;
133             nt.pre=te.index;
134             nt.step=te.step+1;
135             if(yy.f==0){
136                 nt.cnt++;
137             }
138             if(nt.step>Step[nt.index]) continue;
139             if(nt.step==Step[nt.index] && nt.cnt>Cnt[nt.index]) continue;
140             Step[nt.index]=nt.step;
141             Cnt[nt.index]=nt.cnt;
142             nt.indexn=totnode;
143             node[totnode].in=yy.indexb;
144             node[totnode].pre=te.indexn;
145             totnode++;
146             q.push(nt);
147         }
148     }
149 }
150 
151 void solve()
152 {
153     bfs();
154 }
155 
156 void out(QQ te)
157 {
158     int i;
159     int vis2[N];
160     memset(vis2,0,sizeof(vis2));
161     i=te.indexn;
162     int temp;
163     while(i!=-1)
164     {
165         temp=node[i].in;
166         vis2[temp]=1;
167         i=node[i].pre;
168     }
169     for(i=1;i<=m;i++){
170         if(vis2[i]==1){
171             if(z[i]==0){
172                 ans[tot].a=x[i];
173                 ans[tot].b=y[i];
174                 ans[tot].f=1;
175                 tot++;
176             }
177         }
178         else{
179             if(z[i]==1){
180                 ans[tot].a=x[i];
181                 ans[tot].b=y[i];
182                 ans[tot].f=0;
183                 tot++;
184             }
185         }
186     }
187     printf("%d
",tot);
188     for(i=0;i<tot;i++){
189         printf("%d %d %d
",ans[i].a,ans[i].b,ans[i].f);
190     }
191 }
192 
193 int main()
194 {
195     //freopen("data.in","r",stdin);
196    // freopen("data.out","w",stdout);
197     //scanf("%d",&T);
198     //for(int ccnt=1;ccnt<=T;ccnt++)
199     //while(T--)
200     while(scanf("%d%d",&n,&m)!=EOF)
201     {
202         ini();
203         solve();
204 //        out();
205     }
206     return 0;
207 }

    一开始wa在test8的代码：

      1 #include<iostream>
  2 #include<cstring>
  3 #include<cstdlib>
  4 #include<cstdio>
  5 #include<algorithm>
  6 #include<cmath>
  7 #include<queue>
  8 #include<map>
  9 #include<set>
 10 #include<stack>
 11 #include<string>
 12 
 13 #define N 100005
 14 #define M 105
 15 #define mod 1000000007
 16 //#define p 10000007
 17 #define mod2 1000000000
 18 #define ll long long
 19 #define LL long long
 20 #define eps 1e-6
 21 #define inf 100000000
 22 #define maxi(a,b) (a)>(b)? (a) : (b)
 23 #define mini(a,b) (a)<(b)? (a) : (b)
 24 
 25 using namespace std;
 26 
 27 int n,m;
 28 int x[N],y[N],z[N];
 29 int tot;
 30 
 31 typedef struct
 32 {
 33     int a,b;
 34     int f;
 35 }AA;
 36 
 37 AA ans[N];
 38 
 39 typedef struct
 40 {
 41     int to;
 42     int f;
 43     int indexb;
 44 }PP;
 45 
 46 vector<PP>bian[N];
 47 int vis[N];
 48 int Step[N];
 49 int Cnt[N];
 50 
 51 struct QQ
 52 {
 53     friend bool operator < (QQ n1,QQ n2)
 54     {
 55         if(n1.step==n2.step){
 56             return n1.cnt>n2.cnt;
 57         }
 58         else{
 59             return n1.step>n2.step;
 60         }
 61     }
 62     int index;
 63     int cnt;
 64     string s;
 65     int indexn;
 66     int pre;
 67     int step;
 68 };
 69 
 70 void out(QQ te);
 71 
 72 void ini()
 73 {
 74     int i;
 75     tot=0;
 76     memset(vis,0,sizeof(vis));
 77     PP te;
 78     for(i=1;i<=n;i++){
 79         bian[i].clear();
 80         Step[i]=inf;
 81         Cnt[i]=inf;
 82     }
 83     Step[1]=0;
 84     Cnt[1]=0;
 85     for(i=1;i<=m;i++){
 86         scanf("%d%d%d",&x[i],&y[i],&z[i]);
 87         te.to=y[i];te.f=z[i];te.indexb=i;
 88         bian[ x[i] ].push_back(te);
 89         te.to=x[i];
 90         bian[ y[i] ].push_back(te);
 91     }
 92 }
 93 
 94 typedef struct
 95 {
 96     int in;
 97     int pre;
 98 }NN;
 99 
100 NN node[N*10];
101 int totnode;
102 
103 void bfs()
104 {
105     priority_queue <QQ>q;
106     QQ te,nt;
107     te.index=1;
108     te.cnt=0;
109     te.step=0;
110     te.s="";
111     totnode=0;
112     te.indexn=-1;
113     te.pre=-1;
114     //vis[1]=1;
115     q.push(te);
116     int st;
117     PP yy;
118     char ss;
119     vector<PP>::iterator it;
120     while(q.size()>=1)
121     {
122         te=q.top();
123        // printf(" index=%d cnt=%d",te.index,te.cnt);
124        // cout<<" s="<<te.s<<endl;
125         q.pop();
126         if(te.index==n){
127             out(te);
128             return;
129         }
130         if(vis[te.index]==1) continue;
131         vis[te.index]=1;
132         st=te.index;
133         for(it=bian[st].begin();it!=bian[st].end();it++)
134         {
135             yy=*it;
136             if(vis[yy.to]==1) continue;
137             nt.index=yy.to;
138             ss=yy.indexb+'0';
139             nt.s=te.s+ss;
140            // vis[yy.indexb]=1;
141             //vis[nt.index]=1;
142             nt.cnt=te.cnt;
143             nt.pre=te.index;
144             nt.step=te.step+1;
145             if(yy.f==0){
146                 nt.cnt++;
147             }
148             if(nt.step>Step[nt.index]) continue;
149             if(nt.step==Step[nt.index] && nt.cnt>Cnt[nt.index]) continue;
150             Step[nt.index]=nt.step;
151             Cnt[nt.index]=nt.cnt;
152             nt.indexn=totnode;
153             node[totnode].in=yy.indexb;
154             node[totnode].pre=te.indexn;
155             totnode++;
156             q.push(nt);
157 
158            // printf("  index=%d cnt=%d",nt.index,nt.cnt);
159           //  cout<<" s="<<nt.s<<endl;
160         }
161     }
162 }
163 
164 void solve()
165 {
166     bfs();
167 }
168 
169 void out(QQ te)
170 {
171     int l=te.s.length();
172     int i;
173     int vis2[N];
174     memset(vis2,0,sizeof(vis2));
175    // cout<<"te.s="<<te.s<<" l="<<l<<endl;
176     i=te.indexn;
177     int temp;
178     while(i!=-1)
179     {
180         temp=node[i].in;
181         vis2[temp]=1;
182         i=node[i].pre;
183     }
184    // for(i=0;i<l;i++){
185   //      vis2[ te.s[i]-'0' ]=1;
186    // }
187     for(i=1;i<=m;i++){
188         if(vis2[i]==1){
189             if(z[i]==0){
190                 ans[tot].a=x[i];
191                 ans[tot].b=y[i];
192                 ans[tot].f=1;
193                 tot++;
194             }
195         }
196         else{
197             if(z[i]==1){
198                 ans[tot].a=x[i];
199                 ans[tot].b=y[i];
200                 ans[tot].f=0;
201                 tot++;
202             }
203         }
204     }
205     printf("%d
",tot);
206     for(i=0;i<tot;i++){
207         printf("%d %d %d
",ans[i].a,ans[i].b,ans[i].f);
208     }
209 }
210 
211 int main()
212 {
213     //freopen("data.in","r",stdin);
214    // freopen("data.out","w",stdout);
215     //scanf("%d",&T);
216     //for(int ccnt=1;ccnt<=T;ccnt++)
217     //while(T--)
218     while(scanf("%d%d",&n,&m)!=EOF)
219     {
220         ini();
221         solve();
222 //        out();
223     }
224     return 0;
225 }
  • 相关阅读:
    elasticsearch客户端连接选择
    logstash5.x配置
    git操作
    Linux的crontab
    让MySQL支持中文
    Python装饰器（decorator）
    Python类的探讨
    Python对象（译）
    Python基础－作用域和命名空间（Scope and Namespace）
    Python输入输出（IO）
  • 原文地址：https://www.cnblogs.com/njczy2010/p/4250717.html
Copyright © 2011-2022 走看看