冒泡排序

【基本思想】

　　从后往前扫描待排序序列，如果前一个元素比后一个元素大，就交换它们两个，对每一对相邻元素作同样的工作；这样，第一次扫描待排序的序列会找到一个最小值并将其放置在第一位，第二次扫描待排序的序列会找到一个第二小的值并将其放置在第二位，第三次扫描待排序的序列会找到一个第三小的值并将其放置在第三位，以此类推，直到将所有元素排序完毕；排序的过程就像泡泡不断的往上冒，总是小的泡泡在最上面，大的泡泡在最下面。

 

【算法复杂度】

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(n^2)	O(n^2)	O(n)	O(1)	稳定

时间复杂度>>>

若文件的初始状态是正序的，一趟扫描即可完成排序，所需的关键字比较次数  和记录移动次数  均达到最小值：

  

，

  ，

所以，冒泡排序最好的时间复杂度为  。

 

若初始文件是反序的，需要进行

  

趟排序，每趟排序要进行

  

次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。

在这种情况下，比较和移动次数均达到最大值：

 

 

 

综上，冒泡排序的最坏时间复杂度为  ，平均时间复杂度为

  

。

算法稳定性>>>

冒泡排序就是把小的元素往前调或者把大的元素往后调，比较是相邻的两个元素比较，交换也发生在这两个元素之间，所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

【动图演示】

 

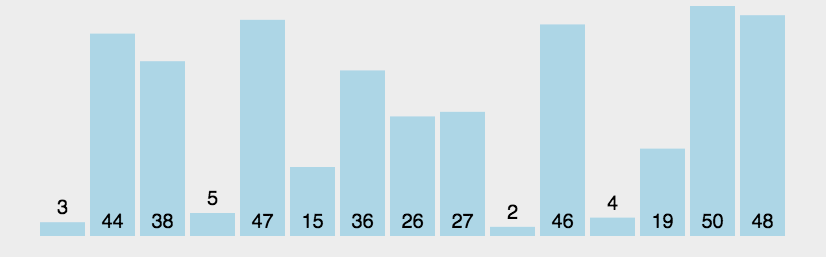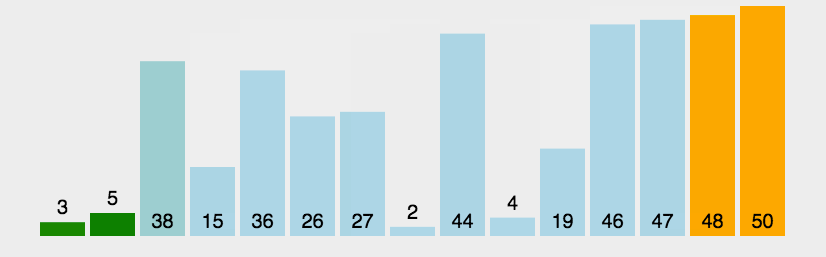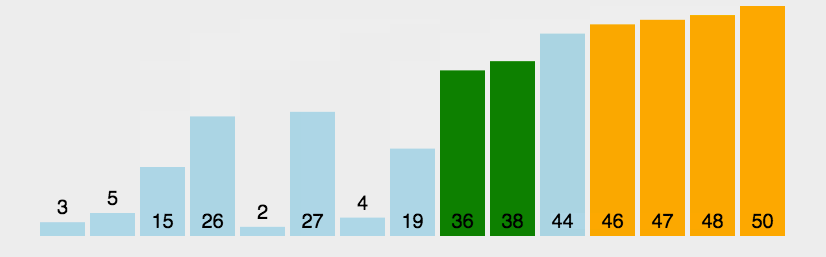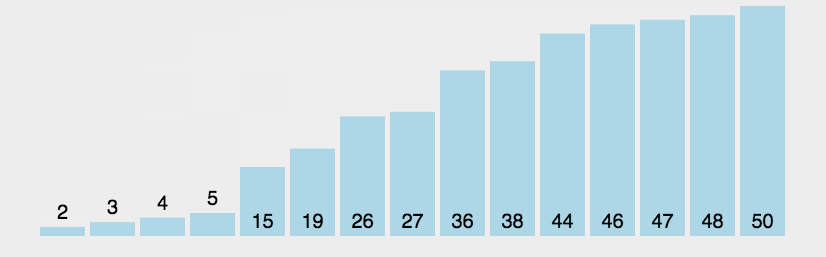
【算法实现】

/*
** 下面是经过优化的冒泡排序算法的具体实现
** 设置标志位以避免对已经有序的序列继续进行排序
** 设置边界值使每趟扫描都在已经排好序的位置处停止比较
*/

void bubbleSort(vector<int>& seq)
{
    int index = 0;    //设置边界值，下一次比较到此处即停止
    int length = seq.size();  //待排序序列的长度
    bool flag = true;   //设置标志位，标志为true则继续进行排序，标志为false则序列已经排好序，终止排序
    for (int i = 0; i < length && flag; i = index) {
        flag = false;
        for (int j = length - 2; j >= i; j--) {
            if (seq[j] > seq[j + 1]) { //前一个元素比后一个元素大，交换这两个元素
                index = j;    //若存在数据交换，设置边界值为j
                seq[j] ^= seq[j + 1];
                seq[j + 1] ^= seq[j];
                seq[j] ^= seq[j + 1];
                flag = true; //若存在数据交换，则序列没有排好序，设置标志为true
            }
        }
    }
}