直接选择排序

 

【基本思想】

　　每一次从待排序的序列中选出最小（或最大）的一个元素，存放在已排好序的序列的后一个位置，直到全部待排序的数据元素排完；

　　例如，给定包含N个正整数元素的序列vector<int> seq
　　　　第1趟：从seq[0]~seq[n-1]中选出最小的数据，将它与seq[0]交换；
　　　　第2趟，从seq[1]~seq[n-1]中选出最小的数据，将它与seq[1]交换；
　　　　第3趟，从seq[2]~seq[n-1]中选出最小的数据，将它与seq[2]交换；
　　　　.... .... .... .... .... ....

　　　　第n-1趟，从seq[n-2]~seq[n-1]中选出最小的数据，将它与seq[n-2]交换。

【算法复杂度】

时间复杂度（平均）	时间复杂度 （最坏）	时间复杂度（最好）	空间复杂度	稳定性
O(n^2)	O(n^2)	O(n^2)	O(1)	不稳定

 

时间复杂度>>>

选择排序的交换操作介于 0 和 (n - 1) 次之间，最好情况是，已经有序，交换0次；最坏情况交换n-1次，逆序交换n/2次；

选择排序比较操作的次数与关键字的初始状态无关，总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。

算法稳定性>>>

选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只

剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。比较拗口，举个例

子，序列5 8 5 2 9，我们知道第一遍选择第元素5会和2交换，那么原序列中两个5的相对前后顺序就被破坏了，所以选择排序是一个不稳定的排序算法。 

【动图演示】

  

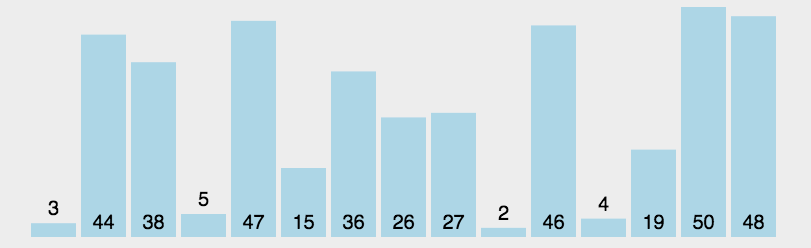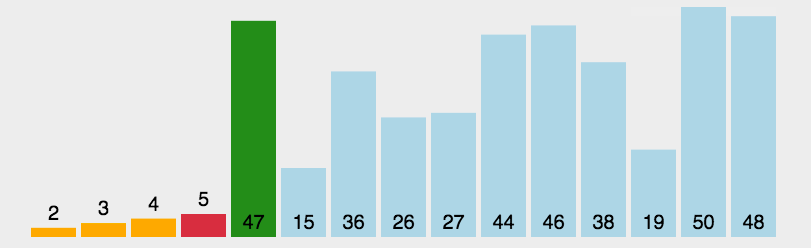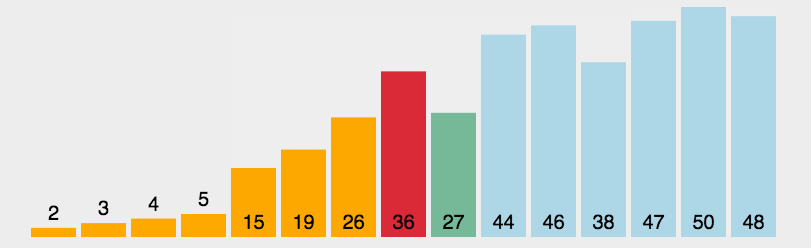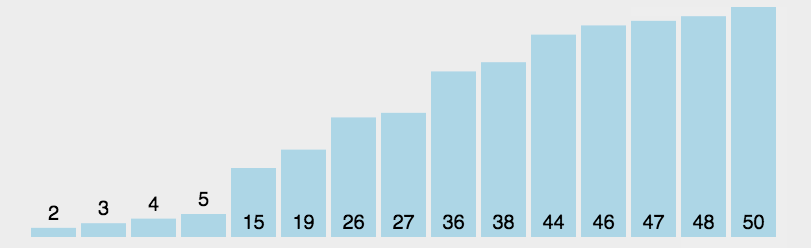
【算法实现】

/*
** 直接选择排序算法的C++实现
*/

void selectSort(vector<int>& seq){
    int length = seq.size();    // 待排序序列的长度
    for(int i=0;i<length-1;i++){
        int min=i,j=i+1;    // min设置为当前最小元素的下标
        for(;j<length;j++)    // 从未排好序的序列中选择最小的元素
            if(seq[j]<=seq[min]) min=j;    

        if(min!=i){      // 设置min!=i防止元素自身与自身交换
            seq[i] ^= seq[min];
            seq[min] ^= seq[i];
            seq[i] ^= seq[min];
        }
    }
}