1 我们拿到一组数据之后就要对它进行模型的直接分析,这种方式是不可取的,因为模型都有自己的假设条件,也就是先前假设,但是数据的状态大多数情况并不符合模型的要求,因此首先要对数据进行变换处理,达到模型对数据的要求。这样模型对于数据处理的结果才具有可参考性。因此很多人只关心和研究模型,而忽略了对数据的处理。
2 原则:
原则1:数据的变换其内涵是转换对于数据的观察角度,而不是经过变形后其原先的内涵产生变化。
原则2:
3 数据标准化的方法:
3.1 Z_score规范化
也就是常说的Z变换,先贴代码:
load lawdata; plot([gpa,lsat])
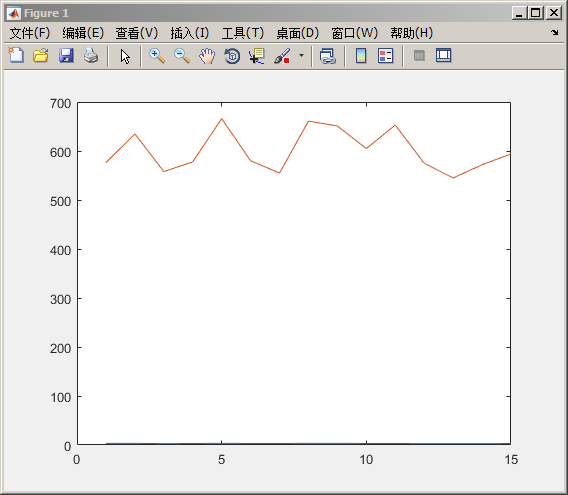
我们观察到两组数据的值差别太大了,如果对这两组数据进行分析很难得到想要的结果,这个时候可以考虑用Z-scores的方式
%% z-scores 变换
clear;clc;
load lawdata;
plot([gpa,lsat])
% z-score变换
gpa_mean = mean(gpa);
gpa_std = std(gpa);
for i = 1:length(gpa)
Zgpa1(i,1) = (gpa(i,1) - gpa_mean) / gpa_std;
end
Zgpa = zscore(gpa);
disp([Zgpa1';Zgpa'])
% % 显示结果:
% 1 至 6 列
% 1.2128 0.8432 -1.1690 -0.2656 1.4181 -0.1013
% 1.2128 0.8432 -1.1690 -0.2656 1.4181 -0.1013
% 7 至 12 列
% -0.3888 1.3771 1.0896 0.1451 0.1040 -1.4565
% -0.3888 1.3771 1.0896 0.1451 0.1040 -1.4565
% 13 至 15 列
% -1.3743 -0.8815 -0.5530
% -1.3743 -0.8815 -0.5530
我们通过公式和MATLAB自带函数计算的结果一致,对于lsat就不公式计算了,直接得到两组数据的结果如下:
Zgpa = zscore(gpa);
Zlsat = zscore(lsat);
plot([Zgpa, Zlsat])
legend('gpa z-scores','lsat z-scores','Location','Northeast')
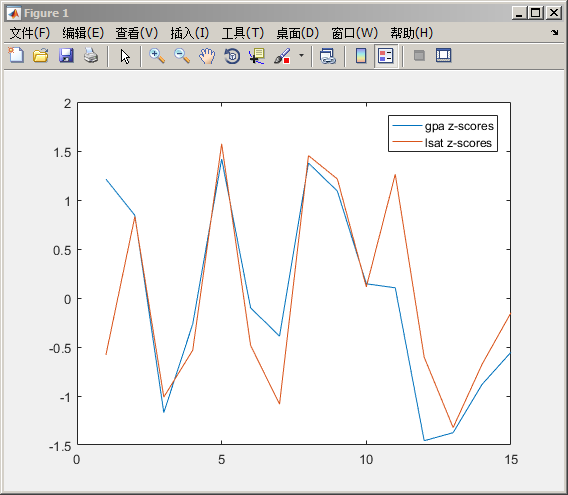
结果:这样对于两组数据进行评价,就容易进行比较了。
小结:
1 如果两组以上的数据值差别较大时(一般都有较大差别),引入z-scores这把“尺子”,能够容易衡量不同组向量之间的关系。
2 这种方式一般用于多组向量值之间的比较比较合适。
3.2 中心化
这种做法是经过中心化变化之后,均值为0,但是方差矩阵不变。
代码如下:
%% 中心化
clear;clc;
load lawdata;
gpa_mean = mean(gpa);
gpa_lsat = mean(lsat);
for i = 1:length(gpa)
Zgpa(i,1) = (gpa(i,1) - gpa_mean);
end
for i = 1:length(lsat)
Zlsat(i,1) = (lsat(i,1) - gpa_lsat);
end
subplot(221)
plot(gpa)
title('gpa非中心化处理')
subplot(223)
plot(Zgpa)
title('gpa中心化处理')
subplot(222)
plot(lsat)
title('lsat非中心化处理')
subplot(224)
plot(Zlsat)
title('lsat中心化处理')

小结:
1 这种处理方式可以理解为分位的处理方式,用均值把数据一分为二的处理。处理单一数据比较合适。
3.3 极差标准化:
我们运用了极值的方法,代码如下:
%% 极差标准化
clear;clc;
load lawdata;
gpa_mean = mean(gpa);
gpa_limit = max(gpa) - min(gpa);
lsat_mean = mean(lsat);
lsat_limit = max(lsat) - min(lsat);
for i = 1:length(gpa)
Cgpa(i,1) = (gpa(i,1) - gpa_mean) / gpa_limit;
end
for i = 1:length(lsat)
Clsat(i,1) = (lsat(i,1) - lsat_mean) / lsat_limit;
end
subplot(221)
plot(gpa)
title('gpa非极差处理')
subplot(223)
plot(Cgpa)
title('gpa极差处理')
subplot(222)
plot(lsat)
title('lsat非极差处理')
subplot(224)
plot(Clsat)
title('lsat极差处理')

小结:
1 发现极差处理化的方法和中心化处理的方法不同之处在于,对于分位都会限制在一定的范围之内,可以统一两组数据进行标准化比较。
3.4 小数规范化(略)
3.5 Box_Cox变换(重点)
Box和Cox是两位大牛在1964年从实际数据出发提出了一种很有效的变化,分常见变化和拓展变化:
作用:
*改变分布形状,使之正太分布,至少是对称的。
*当X>=0时,能够保持数据大小次序
*对变换结果有很好的解释:
1.k = 2 为平方变换
2.k=1 为恒等变换
3.k=0.5平方根变换
4.k=-0.5为平方根倒数变换
5.k=0为对数变换
6.k=-1为倒数变换
If λ is not = 0, then
data(λ)=dataλ−1λ
If λ is = 0, then
data(λ)=log(data)
当然MATLAB工具箱也提供这种变化的函数,先贴代码:
%% Box_Cox变换
clear;clc;
textdata = []; % 手工导入一个交易时间段的close数据
BCtextdata = boxcox(textdata);
subplot(221)
plot(textdata)
title('非Box\_cox处理')
subplot(223)
plot(BCtextdata)
title('Box\_cox处理')
subplot(222)
hist(textdata)
title('未Box\_cox处理后直方图')
subplot(224)
hist(BCtextdata)
title('Box\_cox处理后直方图')
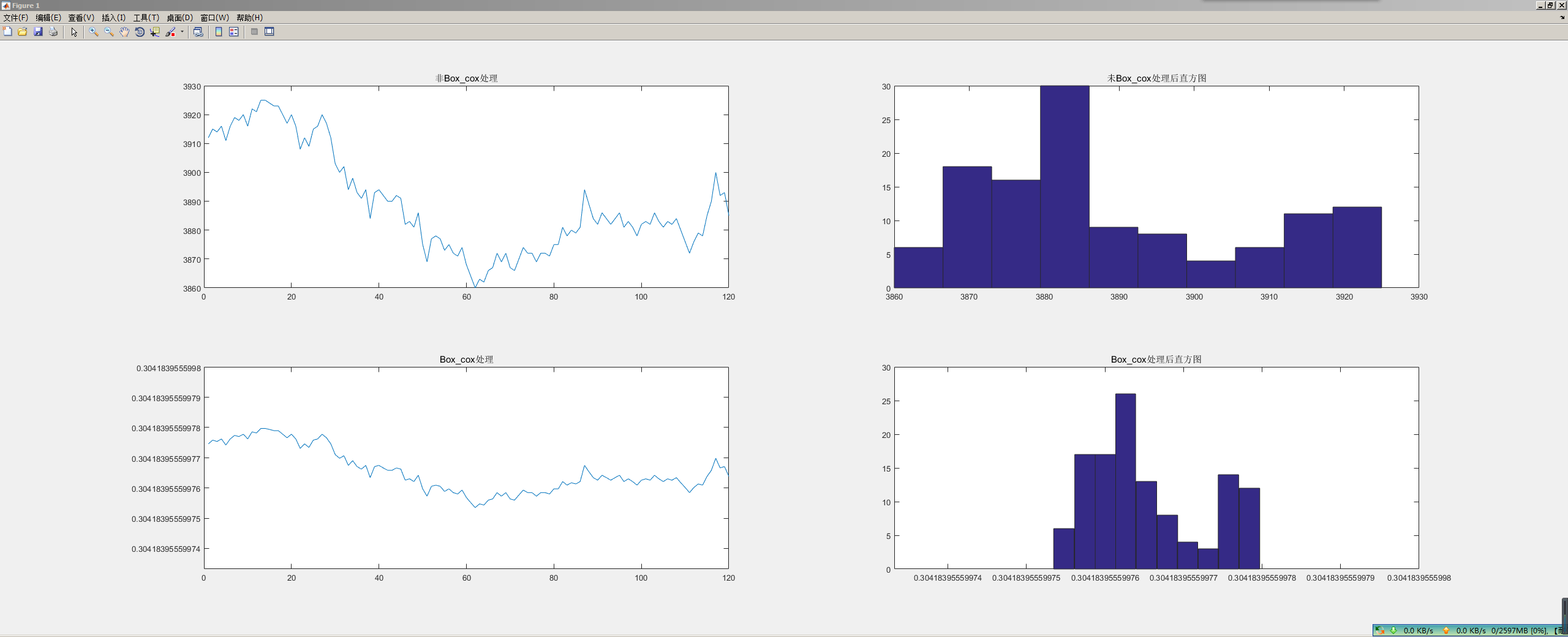
小结:
1 这里注意用boxcox处理方式,数值必须是正值
4 另外,我们再用一种处理方式——差分(扫地僧一般的存在)
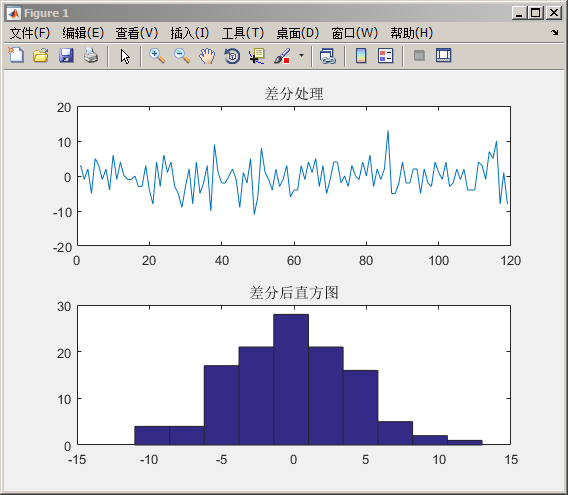
我们对任意一组数据进行差分处理,看到一个惊人的现象没?
但是还有这种情况:
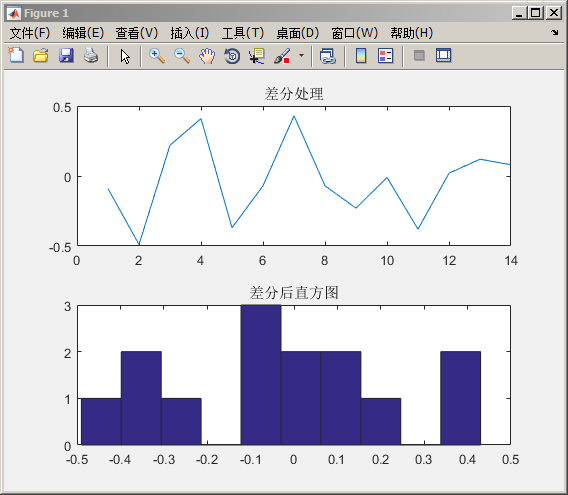
但是这种情况还有:
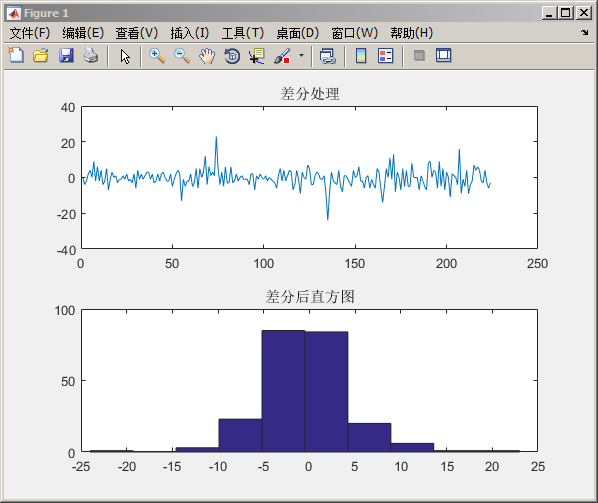
神器:
我们得到一个证明:如果当数据足够大的时候(4的第二幅图数组15个,不符合要求)。经过一阶差分后,会接近正太分布。这是符合大数定理的原则。因此要处理数据的时候,当我们数据足够多的时候,经过一阶差分,数据就可以得到正太数据的近似要求!上面的实验是一个非常好的证明!