Atlantis
题目大意:给n个矩形,求出矩形面积并
经典入门扫描线。首先我们来看什么是扫描线。
扫描线,是一条我们构造的一条垂直于坐标轴的线,目的是将矩形面积并的问题分割为求若干矩形的问题。
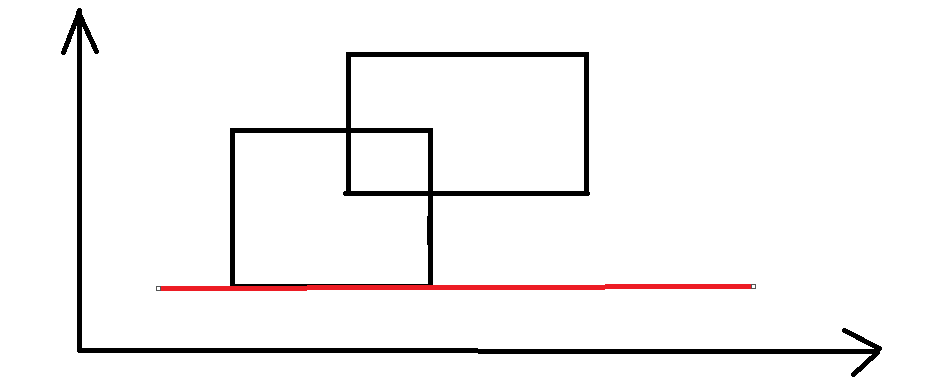
如上图,两个矩形相交,红色的线即为我们的扫描线,扫描线可以垂直于y轴也可以垂直于x轴,我们将以垂直于y轴作为标准讲解。
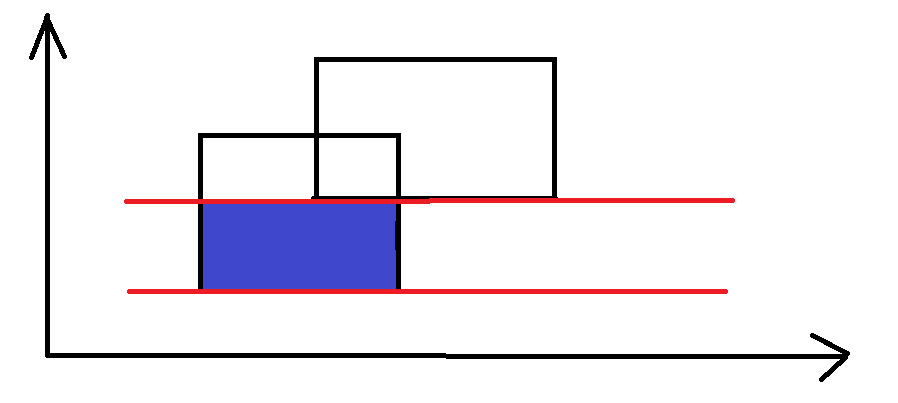
如上图,我们当前可以求出蓝色矩形的面积,这是第一块的面积。
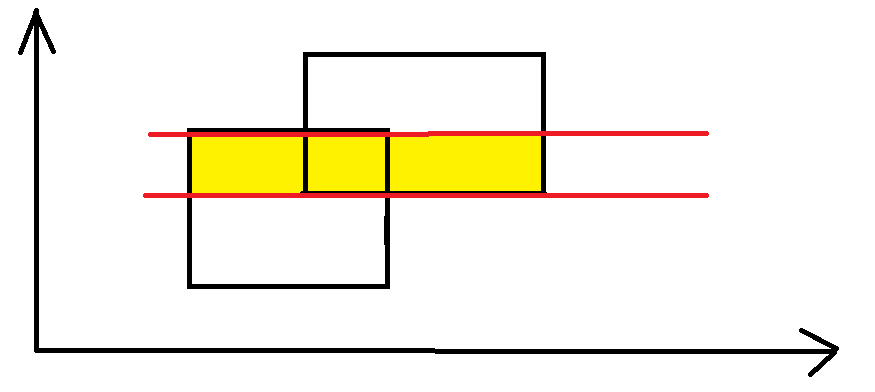
接下来,又求得黄色矩形的面积。
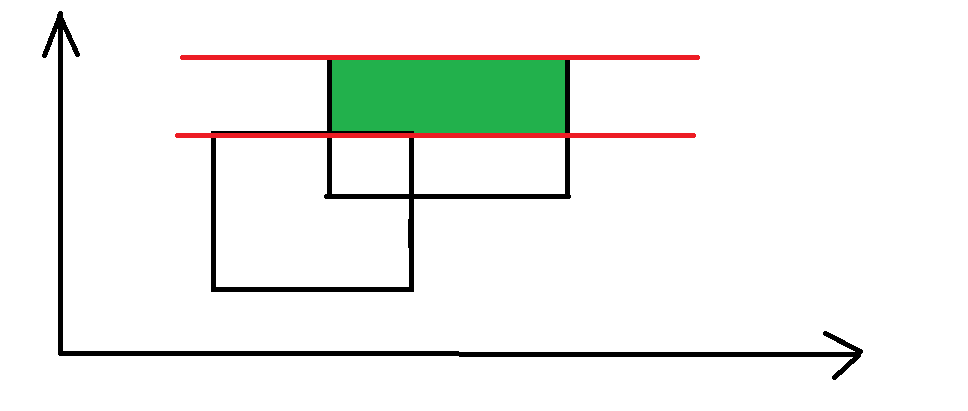
最后,我们求得绿色矩形的面积,所以答案很容易得到为三次求得面积的和。
要提的是,我们的扫描线其实只有一条,而图中画出两条是为了更好看出我们每次计算的面积是哪一部分。而我们每次扫描一条线的时ans+=(下一条线的高度-当前高度)*当前高度的x的长度。

以这张图为例,我当前扫描线其实是下方的红线,我的当前高度的长度为该矩形的长,下一条线的高度减去当前高度为矩形的宽。

当计算绿色矩形面积时,我们的扫描线为下方红线,很明显下方红线穿过的长度大于上方红线穿过的长度,如果我们还想刚才那样做ans+=。就会有多余面积,为了解决这一问题,我们将矩形的上底和下底用不同标记来表示,通常下底标为1,上底标为-1。当我们扫到标记为-1的边时我们要将这条边减去,同时我们也会有数组来存当前的标记值为多少。
代码如下:
#include<cstdio> #include<algorithm> #include<cstring> using namespace std; int n,m=0; int mark[2000],lt[2000],rt[2000]; double nex[2000],s[2000]; struct node{ double l,r,h; int f; //标记上底还是下底 }a[1000]; bool cmp(node a,node b) { return a.h<b.h; } void build(int l,int r,int k) { mark[k]=0,s[k]=0; lt[k]=l;rt[k]=r; if(l==r-1) return; int mid=(l+r)/2; build(l,mid,k<<1); build(mid,r,k<<1|1); } void init() { m=0; for(int i=1;i<=n;i++) { double x1,y1,x2,y2; scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); a[m].l=x1;a[m].r=x2;a[m].h=y1; a[m].f=1;nex[m]=x1;m++; a[m].l=x1;a[m].r=x2;a[m].h=y2; a[m].f=-1;nex[m]=x2;m++; } sort(a,a+m,cmp); sort(nex,nex+m); m=unique(nex,nex+m)-nex; build(0,m-1,1); } void update(int k) { if (mark[k]) s[k]=nex[rt[k]]-nex[lt[k]]; else if (rt[k]==lt[k]) s[k]=0; else s[k]=s[k<<1]+s[k<<1|1]; } void change(int l,int r,int k,int flag) { if(l<=lt[k]&&r>=rt[k]) { mark[k]+=flag; update(k); return ; } int mid=(lt[k]+rt[k])/2; if(l>=mid) { change(l,r,k<<1|1,flag); } else if(r<=mid) { change(l,r,k<<1,flag); } else { change(l,r,k<<1,flag); change(l,r,k<<1|1,flag); } update(k); } int main() { int cnt=0; while(scanf("%d",&n)!=EOF&&n) { init(); double ans=0; for(int i=0;i<=2*n-1;i++) { int l=lower_bound(nex,nex+m,a[i].l)-nex; int r=lower_bound(nex,nex+m,a[i].r)-nex; change(l,r,1,a[i].f); ans+=s[1]*(a[i+1].h-a[i].h); } printf("Test case #%d ",++cnt); printf("Total explored area: %.2f ",ans); } return 0; }
之后有想法会继续写全一点(其实是现在太菜解释不来