题目背景
给一组 N 枚邮票的面值集合(如,{1 分,3 分})和一个上限 K —— 表示信封上能够贴 K 张邮票。计算从 1 到 M 的最大连续可贴出的邮资。
题目描述
例如,假设有 1 分和 3 分的邮票;你最多可以贴 5 张邮票。很容易贴出 1 到 5 分的邮资(用 1 分邮票贴就行了),接下来的邮资也不难:
6 = 3 + 3
7 = 3 + 3 + 1
8 = 3 + 3 + 1 + 1
9 = 3 + 3 + 3
10 = 3 + 3 + 3 + 1
11 = 3 + 3 + 3 + 1 + 1
12 = 3 + 3 + 3 + 3
13 = 3 + 3 + 3 + 3 + 1然而,使用 5 枚 1 分或者 3 分的邮票根本不可能贴出 14 分的邮资。因此,对于这两种邮票的集合和上限 K=5,答案是 M=13。 [规模最大的一个点的时限是3s]
小提示:因为14贴不出来,所以最高上限是13而不是15
输入输出格式
输入格式:
第 1 行: 两个整数,K 和 N。K(1 <= K <= 200)是可用的邮票总数。N(1 <= N <= 50)是邮票面值的数量。
第 2 行 .. 文件末: N 个整数,每行 15 个,列出所有的 N 个邮票的面值,每张邮票的面值不超过 10000。
输出格式:
第 1 行:一个整数,从 1 分开始连续的可用集合中不多于 K 张邮票贴出的邮资数。
输入输出样例
说明
题目翻译来自NOCOW。
USACO Training Section 3.1
---------------------------------------------------------------------------------------------------
分析:用dp[i]表示最少用几张牌组成i方程,需要一个小技巧:我们可以将k这个条件转化成求什么时候,需要组成数字i的牌数>k。
剩下的话,不难想到,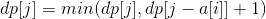 ,用这个式子跑循环就可以了。
,用这个式子跑循环就可以了。
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 const int maxn=2000005; 5 int dp[maxn],a[100];//dp[i]:用几张牌组成i 6 int main() 7 { 8 int n,k; 9 scanf("%d%d",&k,&n); 10 for(int i=1;i<=n;i++) 11 { 12 scanf("%d",&a[i]); 13 } 14 for(int i=0;i<maxn;i++) dp[i]=999999999; 15 dp[0]=0; 16 for(int i=1;i<=n;i++) 17 { 18 for(int j=a[i];j<=maxn;j++) 19 { 20 dp[j]=min(dp[j],dp[j-a[i]]+1); 21 } 22 } 23 for(int i=1;i<=maxn;i++) 24 { 25 if(dp[i]>k||dp[i]<1) 26 { 27 printf("%d ",i-1); 28 return 0; 29 } 30 } 31 return 0; 32 }