VC Dimension -衡量模型与样本的复杂度

(1)定义VC Dimension：

dichotomies数量的上限是成长函数，成长函数的上限是边界函数：

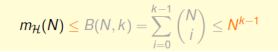
所以VC Bound可以改写成：

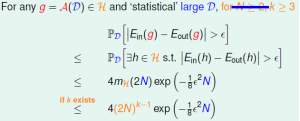
下面我们定义VC Dimension：

对于某个备选函数集H，VC Dimension就是它所能shatter的最大数据个数N。VC Dimension = minimum break point - 1。所以在VC Bound中，(2N)^(k-1)可以替换为(2N)^(VC Dimension)。VC Dimension与学习算法A，输入分布P，目标函数f均无关。

(2)PLA的VC Dimension  

1D的PLA最多shatter2个点，所以VC Dimension = 2；      

2D的PLA最多shatter3个点，所以VC Dimension = 3；                                                       

猜测dD的PLA，VC Dimension会不会等于d+1？ 只需证明d_vc≥d+1并且 d_vc≤d+1

• 证明VC Dimension≥d+1，只需证明H可以shatter某些d+1个输入。

构造一组d+1个输入：

 X=

第一列灰色的1是对每个输入提高1维的操作，这个是一个d+1维的方阵，对角线全部是1，所以该矩阵可逆。即对于任意一种输出，我们总能找到一个备选函数使得

 

图2 

即这一组输入的所有dichotomies都被穷尽了，所以VC Dimension≥d+1得证

• 证明VCDimension≤d+1，只需证H不能shatter任何d+2个输入

在2D情形下构造一组4个输入：

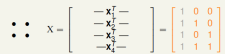
图3

所以 x₄ = x₃ + x₂ - x₁