Codeforces Round #645 (Div. 2) A

题目链接

---

(A. Park Lighting)

(Description:)
  给出 (n imes m) 的矩阵，你需要用灯照亮矩阵的每个单元格，灯只能摆放在单元格的边框上（具体参考原题里的图），如果某个单元格的边框上有一盏灯，那么该单元格将被照亮，问最少需要多少个单元格？
(Solution:)
  贪心即可。
(Code:)

/*
@Author: nonameless
@Date:   2020-05-27 15:54:25
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
const double PI  = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }


int main(){

    int t; cin >> t;
    while(t --){
        int n, m; cin >> n >> m;
        int ans = 0;
        ans = n / 2 * m;
        if(n & 1){
            ans += m / 2 + (m % 2);
        }
        cout << ans << endl;
    }
    return 0;
}

(B. Maria Breaks the Self-isolation)

(Description:)
  给定长度为 (n) 的数组 (a)，现有一个院子，院子里最初有一个人，那么他要叫其他 (n) 个人来，每个人来的条件是 (a_i leq) 院子里的人 (+) 和他一起来的人的个数（可以一次叫多个人来），问最后院子里最多有几个人？
(Solution:)
  给 (a) 排序，从小到大遍历一边，如果对于 (i) 来说，他不满足条件，那么我们就让他等待（即等后面的人一起去），直到遇到 (j) 满足 (a_j leq cnt + ans)，(cnt) 是当前等待的人，(ans) 是当前院子里的人数。此时 (j) 是满足条件的，那么由于 (a_i leq a_j)，那么 (i) 显然也是符合条件的。
(Code:)

/*
@Author: nonameless
@Date:   2020-05-27 16:00:38
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
const double PI  = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }


int main(){

    int t; cin>> t;
    while(t --){
        vector<int> vec;
        int n; cin >> n;
        for(int i = 1; i <= n; i ++){
            int x; scanf("%d", &x);
            vec.pb(x);
        }
        sort(all(vec));
        int ans = 1, cnt = 0; // cnt 是未进去的
        for(int i = 0; i < sz(vec); i ++){
            if(vec[i] <= ans + cnt){
                ans += cnt + 1;
                cnt = 0; // 全部进去
            } else cnt ++; // 等待的人的个数 ++
        } 

        cout << ans << endl;

    }
    return 0;
}

(C. Celex Update)

(Description:)
  给定如下矩阵：

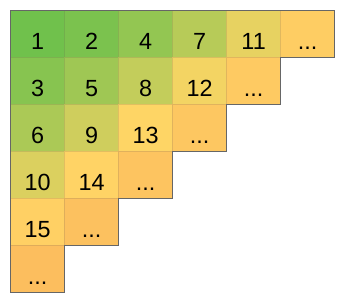
  给定 ((x_1,y_1),(x_2,y_2))，从 ((x_1,y_1)) 走到 ((x_2,y_2))，可以向右和向下走，显然有多条路径，对于一条路径上的各个数字，我们可以求出他的和，问有几个不同的和？
(Solution:)
  最开始光凭脑袋想一点思路没有，然后动手模拟了几遍，就发现了规律：

1. 先一直向右走，再一直向下走，就得到了最小值
2. 先一直向下走，再一直向右走，就得到了最大值
   那么我们用最大值 (-) 最小值 (+1) 就是答案了。那么我们要如何求到了，通过观察可以发现对于上面两种方式走的每一步，都会产生差值：(0,1,2,3,...,x,x,x,x...,x-1,x-2,...,0)。该数列的和 (=) 最大值减去最小值，设 (t) 是我们一共走的步数，那么 (t = x_2-x_1+y_2-y_1)，那么由 (0) 到 (x-1) 和 (x-1) 到 (0) 一共有 (2x) 个数，即还剩下 (t - 2x) 个 (x)，通过观察可以发现 (x = min(x_2-x_1,y_2-y_1))，那么设 (a = min(x_2-x_1,y_2-y_1); b = max(x_2-x_1,y_2-y_1))，即 (x = a)，且 (t = a + b)，那么总和就为:

[ 2 imes frac{(0+a-1) imes a}{2} + (a+b-2a) imes a = a imes b ]

  最后别忘了 (+1)。

(Code:)

/*
@Author: nonameless
@Date:   2020-05-27 20:14:51
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
const double PI  = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }


int main(){

    int t; cin >> t;
    while(t --){
        ll x1, x2, y1, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << (x2 - x1) * (y2 - y1) + 1 << endl;
    }
    return 0;
}

(D. The Best Vacation)

(Description:)
  一年有 (n) 个月，每个月有 (d[i]) 天，其中，第 (j) 的价值为 (j)，问连续 (x) 天的价值最大可以是多少？(可以跨年)
(Solution:)
  要想价值最大，那我们显然是要选择到 (d[i]) 这一天的，即月尾，那么月尾是放在中间还是最后一天呢？对于放在中间，后续还有一系列的数，但显然价值都是很小的，因为又是从 (1) 开始的了，所以我们考虑把月尾放在最后一天，然后我们遍历每个月即可。
(Code:)

/*
@Author: nonameless
@Date:   2020-05-28 14:27:16
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
const double PI  = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }

const int N = 2e5 + 10;

int n;
ll x, sd[N * 2], v[N * 2], sv[N * 2];
int d[N * 2];

int main(){
    cin >> n >> x;
    for(int i = 1; i <= n; i ++){
        scanf("%d", &d[i]);
        d[i + n] = d[i]; // 由于是循环的，但 x < d1 + d2 + .. + dn 的，所以我们存两遍即可
    }
    sd[0] = 0; // 前缀和数组
    for(int i = 1; i <= n + n; i ++) {
        sd[i] = sd[i - 1] + d[i];
        v[i] = 1ll * d[i] * (d[i] + 1) / 2; // v[i] 是对于 i 这个月的总价值
        sv[i] = sv[i - 1] + v[i]; // 前缀和
    }

    ll ans = 0;

    for(int i = n + 1; i <= n + n; i ++){
        ll t = sd[i] - x; // 从第 i 个月最后一天往前走 x 天
        // 最后停止第 j 个月，也就是说从第 j 个月的某一天开始到 第 i 月的最后一天
        int j = lower_bound(sd + 1, sd + 2 * n + 1, t) - sd;
        ll s = sd[i] - sd[j]; // 算出 [j + 1, i] 共多少天
        t = x - s; // 在第 j 个月还有 t 天
        ll tmp = sv[i] - sv[j]; // 这里是 [j + 1, i] 的总价值
        tmp += 1ll * (d[j] + d[j] - t + 1) * t / 2; // 加上第 j 个月的 t 天
        ans = max(ans, tmp);  
    //    printf("i = %d j = %d t = %lld
", i, j, t);
    }
    
    cout << ans << endl;
    

    return 0;
}

(E. Are You Fired?)

(Description:)
  给定长度为 (n) 的数组 (a)，问是否存在一个 (k) 使得数组任意一个长度为 (k) 的子序列的和 (>0)，特别的是：数组中区间为 ([frac{n+1}{2}+1, n]) 的数都为 (x)。
(Solution:)
  由于后面的数都是一样的，比较特殊，所以我们可以从这里突破。设 (sum[i]) 代表 ([1,i]) 的和

1. (x > 0)
   1. (sum[n] leq 0)
      显然是无解的
   2. (sum[n] > 0)
      (k = n)
2. (x leq 0)
   设 (m = n - frac{n+1}{2})，那么 (k > m)，否则在 ([m+1,n]) 就存在一个长度为 (k) 的子序列的和 (leq 0)。那么我们遍历一遍，算出 (k) 的一个可行范围即可。首先假设 (k = n)，对于 (i = 1) 来说，和就是 (sum[k])，大于 (0) 就不要管，如果 (leq 0)，那么我们就需要 (-x)，来使和变大，随之 (k --)，直到 (sum[k] > 0)，接下来一次类推。
   (Code:)

/*
@Author: nonameless
@Date:   2020-05-28 15:50:31
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define all(x) x.begin(), x.end()
#define sz(x) (int)x.size()
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
typedef pair<ll, ll> PLL;
const double PI  = acos(-1.0);
const double eps = 1e-8;
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }

const int N = 5e5 + 10;

int n, x;
int a[N];
ll sum[N];

int main(){

    cin >> n;

    int m = n + 1 >> 1;

    for(int i = 1; i <= m; i ++){
        scanf("%d", &a[i]);
        sum[i] = sum[i - 1] + a[i];
    }

    scanf("%d", &x);
    for(int i = m + 1; i <= n; i ++){
        a[i] = x;
        sum[i] = sum[i - 1] + x;
    }

    if(x > 0){
        if(sum[n] > 0) cout << n << endl;
        else puts("-1");
    } else{
        int k = n;
        m = n - m;
        for(int l = 1; l <= n; l ++){
            int r = l + k - 1; // 区间的右端点
            if(r > n) break; 
            ll tmp = sum[r] - sum[l - 1]; // [l, r] 的和
            while(tmp <= 0 && k > m) tmp -= x, k --;
            if(k <= m) break;
        }
        if(k <= m) puts("-1");
        else cout << k << endl;
    }
    
    return 0;
}