判断题
1.在一个有权无向图中,若b到a的最短路径距离是12,且c到b之间存在一条权为2的边,则c到a的最短路径距离一定不小于10。
当c在a到b的最短路径上时,c到a的路径最小,此时恰好是10。
2.P 是顶点 S 到 T 的最短路径,如果该图中的所有路径的权值都加 1,P 仍然是 S 到 T 的最短路径。
假如说最短路径上一共有10条边,而另一条路径虽然比最短路径长,但它只有一条边,如果全加1,就会导致边少的路径成为新的最短路径。
3.对于带权无向图 G = (V, E),M 是 G 的最小生成树,则 M 中任意两点 V1 到 V2 的路径一定是它们之间的最短路径。
最小生成树只能说明整个路径是最小,并不能说明到单个结点的路径是最小的。
4.Let P be the shortest path from S to T. If the weight of every edge in the graph is incremented by 1, P will still be the shortest path from S to T.
同第2题
5.Let M be the minimum spanning tree of a weighted graph G. Then the path in M between V1 and V2 must be the shortest path between them in G.
同第3题
选择题
1.在一个有权无向图中,如果顶点b到顶点a的最短路径长度是10,顶点c与顶点b之间存在一条长度为3的边。那么下列说法中有几句是正确的?
- c与a的最短路径长度就是13
- c与a的最短路径长度就是7
- c与a的最短路径长度不超过13
- c与a的最短路径不小于7
B.2句
C.3句
D.4句
就是说法太绝对,所以1和2肯定错,3和4可以类似于判断题第一题的分析。
2.若要求在找到从S到其他顶点最短路的同时,还给出不同的最短路的条数,我们可以将Dijkstra算法略作修改,增加一个count[]数组:count[V]记录S到顶点V的最短路径有多少条。则count[V]应该被初始化为:
B.对所有顶点都有count[V]=0
C.count[S]=1;对于其他顶点V则令count[V]=0
D.count[S]=0;对于其他顶点V则令count[V]=1
由于S到S一定有一条长度为0的边,所以count初始化为1,其他则是0
3.我们用一个有向图来表示航空公司所有航班的航线。下列哪种算法最适合解决找给定两城市间最经济的飞行路线问题?
B.Kruskal算法
C.深度优先搜索
D.拓扑排序算法
求最短路径
4.In a weighted graph, if the length of the shortest path from b to a is 10, and there exists an edge of weight 3 between c and b, then how many of the following statements is/are TRUE?
- The length of the shortest path from c to a must be 13.
- The length of the shortest path from c to a must be 7.
- The length of the shortest path from c to a must be no greater than 13.
- The length of the shortest path from c to a must be no less than 7.
B.2
C.3
D.4
同第1题
5.数据结构中Dijkstra算法用来解决哪个问题?
B.最短路径
C.拓扑排序
D.字符串匹配
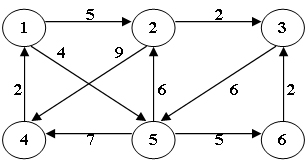
6.使用迪杰斯特拉(Dijkstra)算法求下图中从顶点1到其他各顶点的最短路径,依次得到的各最短路径的目标顶点是:
B.5, 2, 3, 6, 4
C.5, 2, 4, 3, 6
D.5, 2, 6, 3, 4
对于dijkstra算法来说,只有当一个点的所有入度都被遍历过之后,才能完全确认起点到这个点的距离。但这道题没有那么严谨,它的意思似乎仅仅是给各最短路径排序,从短到长。
7.若要求在找到从S到其他顶点最短路的同时,还给出不同的最短路的条数,我们可以将Dijkstra算法略作修改,增加一个count[]数组:count[V]记录S到顶点V的最短路径有多少条。则count[V]应该被初始化为:
B.count[S]=0;对于其他顶点V则令count[V]=1
C.对所有顶点都有count[V]=1
D.对所有顶点都有count[V]=0
同第2题
8.下面的哪个算法可以求图的最短路径____。
B.Dijkstra算法
C.Prim算法
D.哈夫曼算法
9.If an undirected graph G = (V, E) contains 7 vertices. Then to guarantee that G is connected in any cases, there has to be at least __ edges.
B.15
C.16
D.21
为了让第一个结点和第二个结点相连,需要一条边;为了让第三个点和他们相连,需要一条边;为了让第四个点和他们相连,一条边可能不会让他们相连,因为前三个点需要全连接才能保证再加入一条边就让第四个点和他们相连。
那么这个问题就很清晰了,为了求7个点需要几条边,先让前6个点全连接,需要1+2+3+4+5=15个点,然后再加入一条边让第七个边加入。
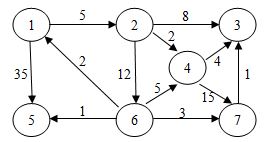
10.使用迪杰斯特拉(Dijkstra)算法求下图中从顶点1到其他各顶点的最短路径,依次得到的各最短路径的目标顶点是:
B.2, 4, 3, 6, 5, 7
C.2, 3, 4, 5, 6, 7
D.5, 2, 6, 3, 4, 7
类似与第6题