据出题的jzh老师所说...
求和
【问题描述】
组合数 C(n,m)是从 n 个物品中取 m 个的方案数。
C(n,m)=(n!)/(m!(n-m)!)
斐波那契数列 F 满足, F[0]=F[1]=1, n≥2 时 F[n]=F[n-1]+F[n-2]
给出 n,求 C(n,0)F[0]+C(n,1)F[1]+…+C(n,n)F[n]
【输入格式】
一行一个数 T 表示数据组数
接下来 T 行每行一个数,表示 n
【输出格式】
输出 T 行, 每行一个数表示答案,对 10^9+7 取模
【样例输入】
3 2 5
1000
【样例输出】
5
89
276439883
【数据规模和约定】
对于 30%的数据, n<=10
对于 60%的数据, n<=1000
对于 100%的数据, T<=1000, n<=10^6
【冷静分析】
30%的点可以暴力过,由于斐波那契最为大家所熟知的是递推式,但其实还有一个直接的通项公式;
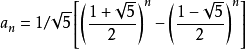
然而本题是一个结论,可以通过以下证明:
