1.相遇
(railway.cpp/c/pas)
时间限制:1s
内存限制:256MB
【问题描述】
已知我国有 n 座城市,这些城市通过 n-1 条高铁相连。且任意两个城市联通。
小 A 想从 x1 号城市出发,到 y1 号城市,小 B 想从 x2 号城市出发,到 y2 号
城市,问他们是否可能在路途中相遇(出现在同一城市)
你需要回答 m 次这样的问题。
【输入】
输入文件名为 railway.in。
第一行一个数 T(<=10),表示数据组数
对于每一组数据:
第一行两个数 n,m(1<=n,m<=100,000)
第 2~n 行,每行两个数 x,y 表示有一条铁路连接城市 x 和 y
接下来 m 行每行四个数,分别表示 x1,y1,x2,y2,表示一次询问
【输出】
输出文件名为 railway.out。
对于每次询问输出 YES 或 NO
【输入输出样例】
| railway.in | railway.out |
| 1 4 2 1 2 2 3 3 4 1 2 3 4 1 4 2 3 |
NO YES |
【数据说明】
对于 30%的数据,n,m<=100
对于 60%的数据,n,m<=1000
对于 100%的数据,n,m<=100,000
太没意思了,树上路径求交,这已经是我近三个月做的第三次了==上次计蒜客刚考过==
考察:LCA+ 分类情况讨论
预计得分:100分
实际得分:100分

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<queue> 5 #include<cmath> 6 #define maxn 100090 7 8 using namespace std; 9 10 int n,m,T,tot,t; 11 int d[maxn],head[maxn],f[maxn][20]; 12 struct node{ 13 int to,next; 14 }edge[maxn*2]; 15 16 void add(int x,int y) 17 { 18 edge[++tot].to=y; 19 edge[tot].next=head[x]; 20 head[x]=tot; 21 } 22 23 void init() 24 { 25 queue<int>q; 26 q.push(1);d[1]=1; 27 while(!q.empty()) 28 { 29 int u=q.front();q.pop(); 30 for(int i=head[u];i;i=edge[i].next) 31 { 32 int v=edge[i].to; 33 if(d[v]) continue; 34 d[v]=d[u]+1; 35 f[v][0]=u; 36 for(int j=1;j<=t;j++) 37 f[v][j]=f[f[v][j-1]][j-1]; 38 q.push(v); 39 } 40 } 41 } 42 43 int lca(int x,int y) 44 { 45 if(d[x]>d[y]) swap(x,y); 46 for(int i=t;i>=0;i--) 47 if(d[f[y][i]]>=d[x]) y=f[y][i]; 48 if(x==y) return x; 49 for(int i=t;i>=0;i--) 50 if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; 51 return f[x][0]; 52 } 53 54 void Clear() 55 { 56 tot=0; 57 memset(head,0,sizeof(head)); 58 memset(d,0,sizeof(d)); 59 memset(f,0,sizeof(f)); 60 } 61 62 int main() 63 { 64 freopen("railway.in","r",stdin); 65 freopen("railway.out","w",stdout); 66 scanf("%d",&T); 67 while(T--) 68 { 69 scanf("%d%d",&n,&m); 70 t=log2(n)+1; 71 for(int i=1;i<=n-1;i++) 72 { 73 int x=0,y=0; 74 scanf("%d%d",&x,&y); 75 add(x,y),add(y,x); 76 } 77 init(); 78 for(int i=1;i<=m;i++) 79 { 80 int a=0,b=0,c=0,e=0; 81 scanf("%d%d%d%d",&a,&b,&c,&e); 82 int p=lca(a,b); 83 int q=lca(c,e); 84 if(p==q) {printf("YES ");continue;} 85 else if(d[p]>d[q]) 86 { 87 if(lca(p,c)==p||lca(p,e)==p) printf("YES "); 88 else printf("NO "); 89 } 90 else 91 { 92 if(lca(q,a)==q||lca(q,b)==q) printf("YES "); 93 else printf("NO "); 94 } 95 } 96 Clear(); 97 } 98 return 0; 99 }
2. 计数
(count.cpp/c/pas)
时间限制: 1s
内存限制: 256MB
【问题描述】
小 A 是一名热衷于优化各种算法的 OIER,有一天他给了你一个随机生成的 1~n 的排列, 并定
义区间[l,r]的价值为: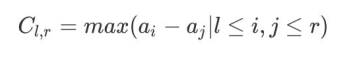
他想请你告诉他, 所有区间的价值的总和为多少
【输入】
输入文件名为 count.in。
第一行一个数 T(<=10), 表示数据组数
对于每一组数据:
第一行一个数 n(1<=n,m<=100,000)
第二行 n 个数 a1...an, 表示一个 1~n 的随机的排列
【输出】
输出文件名为 count.out。
对于每组数据输出一个数, 表示答案
【输入输出样例】
| count.in | count.out |
| 1 4 3 2 4 1 |
14 |
【数据范围】
对于 60%的数据: n<=1000
对于 100%的数据, n<=100,000
考场上想草草n²枚举区间,然后随便找个数据结构维护下区间最值。开始是想用ST表的,但是因为不会打了,所以就只能用线段树了。
预计得分:60分
实际得分:30分
考后发现我的线段树被卡了呜呜,线段树每次查询是logn的,预处理nlogn,所以总复杂度约为O(n²logn)。理论上是可以苟过60分的,但是.......但是......听巨佬们说线段树常数巨大,于是我就被成功卡常了==考后照着写了一遍ST表,就60分了。因为ST表的预处理复杂度同样是nlogn,但是查询是O(1)的。线段树没有修改操作的时候最好不要用的...这个故事告诉我们,多掌握一些知识总是好的==。
Scape:你就是数据结构学傻了。

1 #include<cstdio> 2 #include<algorithm> 3 #define M 100090 4 5 using namespace std; 6 typedef long long ll; 7 8 int T,n; 9 int seq[M]; 10 ll ans; 11 struct SegmentTree{ 12 int l,r; 13 int maxn,minn; 14 }t[M*4]; 15 16 void build(int p,int l,int r) 17 { 18 t[p].l=l,t[p].r=r; 19 if(l==r) 20 { 21 t[p].maxn=seq[l]; 22 t[p].minn=seq[l]; 23 return ; 24 } 25 int mid=(l+r)>>1; 26 build(p*2,l,mid); 27 build(p*2+1,mid+1,r); 28 t[p].maxn=max(t[p*2].maxn,t[p*2+1].maxn); 29 t[p].minn=min(t[p*2].minn,t[p*2+1].minn); 30 } 31 32 int ask1(int p,int l,int r) 33 { 34 if(t[p].l==l&&t[p].r==r) return t[p].maxn; 35 int mid=(t[p].l+t[p].r)>>1; 36 if(l>mid) return ask1(p*2+1,l,r); 37 else if(r<=mid) return ask1(p*2,l,r); 38 else return max(ask1(p*2,l,mid),ask1(p*2+1,mid+1,r)); 39 } 40 41 int ask2(int p,int l,int r) 42 { 43 if(t[p].l==l&&t[p].r==r) return t[p].minn; 44 int mid=(t[p].l+t[p].r)>>1; 45 if(l>mid) return ask2(p*2+1,l,r); 46 else if(r<=mid) return ask2(p*2,l,r); 47 else return min(ask2(p*2,l,mid),ask2(p*2+1,mid+1,r)); 48 } 49 50 int main() 51 { 52 freopen("count.in","r",stdin); 53 freopen("count.out","w",stdout); 54 scanf("%d",&T); 55 while(T--) 56 { 57 scanf("%d",&n); 58 for(int i=1;i<=n;i++) scanf("%d",&seq[i]); 59 build(1,1,n); 60 for(int i=1;i<=n;i++) 61 for(int j=i;j<=n;j++) 62 { 63 if(i==j) continue; 64 int qwq=ask1(1,i,j); 65 int orz=ask2(1,i,j); 66 ans+=qwq-orz; 67 //printf("i:=%d j:=%d %d %d ",i,j,qwq,orz); 68 } 69 printf("%lld ",ans); 70 ans=0; 71 //需不需要清空呢233好慌啊233 72 } 73 return 0; 74 }

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 5 using namespace std; 6 typedef long long ll; 7 8 int T,n; 9 ll ans; 10 int fa[200000][20],fb[200000][20]; 11 12 int sta(int l,int r) 13 { 14 int k=log2(r-l+1); 15 return max(fa[l][k],fa[r-(1<<k)+1][k]); 16 } 17 18 int stb(int l,int r) 19 { 20 int k=log2(r-l+1); 21 return min(fb[l][k],fb[r-(1<<k)+1][k]); 22 } 23 24 int main() 25 { 26 freopen("count.in","r",stdin); 27 freopen("count.out","w",stdout); 28 scanf("%d",&T); 29 while(T--) 30 { 31 scanf("%d",&n); 32 for(int i=1;i<=n;i++) 33 scanf("%d",&fa[i][0]),fb[i][0]=fa[i][0]; 34 for(int j=1;j<=30;j++) 35 for(int i=1;i+(1<<j)-1<=n;i++) 36 fa[i][j]=max(fa[i][j-1],fa[i+(1<<(j-1))][j-1]); 37 for(int j=1;j<=30;j++) 38 for(int i=1;i+(1<<j)-1<=n;i++) 39 fb[i][j]=min(fb[i][j-1],fb[i+(1<<(j-1))][j-1]); 40 for(int i=1;i<=n;i++) 41 for(int j=i+1;j<=n;j++) 42 ans+=sta(i,j)-stb(i,j); 43 printf("%lld ",ans); 44 ans=0; 45 } 46 return 0; 47 }
正解1(By Chemist):分治
我们考虑题目中给出的式子: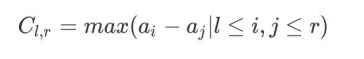
我们可以转化为求所有区间中的最大值,将他们相加;再求出所有区间的最小值,把答案减去他们。
我们考虑找到一个区间中最大值的位置,然后以这个位置为界把区间分成两部分。那么这部分这个最大值作为区间最大值的区间个数就是这个值左边的元素个数x右边的元素个数(可能有点绕qwq)
最小值同理。
之后我们递归求解 ,就能完美地覆盖所有的区间。
枚举区间的最坏复杂度可达到O(n)(据算法作者所述),但是开始Chemist用的是O(n)找区间最值,优化可用st表降低复杂度,但是st表优化的情况只适用于给出的序列互异的情况(是一个排列),因为st表是不能记录位置的,我们需要另开一个数组来映射每个唯一元素的唯一位置。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int M=1e5+10; 5 int n,T,fa[M][30],fb[M][30],pos[M]; 6 ll ans; 7 int sta(int l,int r) 8 { 9 int k=log2(r-l+1); 10 return max(fa[l][k],fa[r-(1<<k)+1][k]); 11 } 12 13 int stb(int l,int r) 14 { 15 int k=log2(r-l+1); 16 return min(fb[l][k],fb[r-(1<<k)+1][k]); 17 } 18 19 void divide1(int l,int r) 20 { 21 if(l>r)return; 22 int mx=0,p=0; 23 mx=sta(l,r); 24 p=pos[mx]; 25 ans+=(ll)mx*(p-l+1)*(r-p+1); 26 divide1(l,p-1); 27 divide1(p+1,r); 28 } 29 void divide2(int l,int r) 30 { 31 if(l>r)return; 32 int mn=1e9,p=0; 33 mn=stb(l,r); 34 p=pos[mn]; 35 ans-=(ll)mn*(p-l+1)*(r-p+1); 36 divide2(l,p-1); 37 divide2(p+1,r); 38 } 39 int main() 40 { 41 freopen("count.in","r",stdin); 42 freopen("count.out","w",stdout); 43 scanf("%d",&T); 44 while(T--) 45 { 46 scanf("%d",&n); 47 for(int i=1;i<=n;i++) 48 scanf("%d",&fa[i][0]),fb[i][0]=fa[i][0],pos[fa[i][0]]=i; 49 for(int j=1;j<=30;j++) 50 for(int i=1;i+(1<<j)-1<=n;i++) 51 fa[i][j]=max(fa[i][j-1],fa[i+(1<<(j-1))][j-1]); 52 for(int j=1;j<=30;j++) 53 for(int i=1;i+(1<<j)-1<=n;i++) 54 fb[i][j]=min(fb[i][j-1],fb[i+(1<<(j-1))][j-1]); 55 divide1(1,n); 56 divide2(1,n); 57 printf("%lld ",ans); 58 ans=0; 59 memset(fa,0,sizeof(fa)); 60 memset(fb,0,sizeof(fb)); 61 } 62 return 0; 63 }
正解2(By miku_sama):单调栈
先%一手炸鲨鱼
维护两个栈:一个保存单调递增的,一个保存单调递减的,大体思路同Chemist.我们每加入一个数,就证明当前的栈顶作最大值的日子到头了==。所以我们加上他所作出的贡献。
结构体里的权值要用longlong,很玄学。

1 #include<cstdio> 2 #include<algorithm> 3 #define maxn 100090 4 5 using namespace std; 6 typedef long long ll; 7 8 int T,n; 9 int a[100090]; 10 ll rmax,rmin; 11 struct sta{ 12 int pos;ll val; 13 }mx[maxn],mi[maxn]; 14 15 int main() 16 { 17 freopen("count.in","r",stdin); 18 freopen("count.out","w",stdout); 19 scanf("%d",&T); 20 while(T--) 21 { 22 scanf("%d",&n); 23 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 24 int maxhead=0,minhead=0; 25 mx[maxhead].pos=0,mx[maxhead].val=1e9; 26 mi[minhead].pos=0,mi[minhead].val=-1; 27 for(int i=1;i<=n;i++) 28 { 29 while(mx[maxhead].val<a[i]) rmax+=mx[maxhead].val*(i-mx[maxhead].pos)*(mx[maxhead].pos-mx[maxhead-1].pos),maxhead--; 30 mx[++maxhead]=(sta){i,a[i]}; 31 while(mi[minhead].val>a[i]) rmin+=mi[minhead].val*(i-mi[minhead].pos)*(mi[minhead].pos-mi[minhead-1].pos),minhead--; 32 mi[++minhead]=(sta){i,a[i]}; 33 } 34 while(maxhead) 35 { 36 rmax+=mx[maxhead].val*(n+1-mx[maxhead].pos)*(mx[maxhead].pos-mx[maxhead-1].pos); 37 maxhead--; 38 } 39 while(minhead) 40 { 41 rmin+=mi[minhead].val*(n+1-mi[minhead].pos)*(mi[minhead].pos-mi[minhead-1].pos); 42 minhead--; 43 } 44 printf("%lld ",rmax-rmin); 45 rmax=0,rmin=0; 46 } 47 return 0; 48 }
***Update:大佬语:神奇之处就在于不是暴力的去找每个区间的最大和最小值,而是逆向统计有多少区间以某个数作为最大和最小值。
3.树上统计
(treecnt.c/cpp/pas)
时间限制: 1s
内存限制: 256MB
【题目描述】
给定一棵n个点的树树。
定义Tree[L,R]表示为了使得L~R号点两两连通, 最少需要选择的边的数量。
求
【输入格式】
第一行一个数, n表示点数(n<=100000)
接下来n-1行每行两个数, x和y, 表示一条连接x号点和y号点的边(x,y<=n)
【输出格式】
输出一个数表示答案
【输入输出样例】
| treecnt.in | treecnt.out |
| 4 1 4 1 3 2 4 |
16 |
【数据范围】
对于20%的数据: n<=10
对于40%的数据: n<=300
对于60%的数据: n<=3000
对于另外20%的数据: 树呈一条链
对于100%的数据: n<=100000
心路历程:
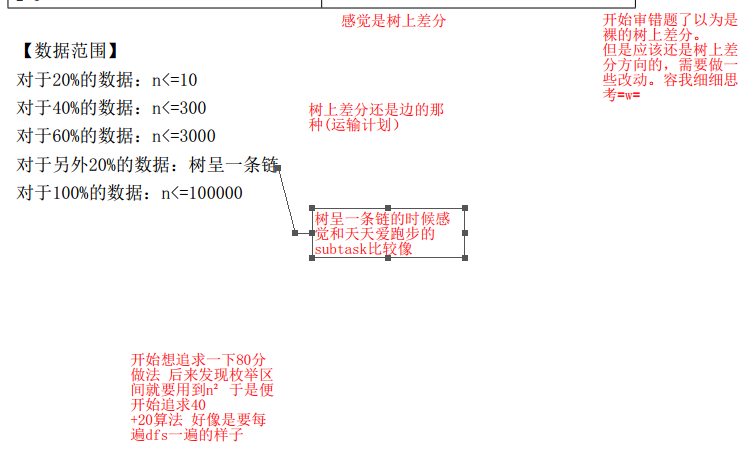
如图,开始想用80分算法的,后来发现60分时枚举区间就需要n²,果断放弃想40分算法,枚举区间用去了n²,那么每次操作就要O(n)内完成。后来想了一想,可以求出这个区间所有点的LCA,然后枚举这个区间的所有点,暴力向上跳,借助求LCA的遗产f数组可以到他的父亲,就还可以dfs一遍记录树上这个节点的前驱编号。(考试时想出了无向边记录一次的方法,感觉很资瓷)。这就O(n)了。区间内所有点的LCA可以预处理求出来,复杂度有保障了。
敲完距考试结束还有大概15分钟的样子,去想链的做法。还是比较好想的,只不过不知道如何判是不是链的情况,根据阅读理解数据范围描述,猜测应该n在3000左右。链时就把它处理成序列,这个节点本应在以它编号作为下标的位置上,现在不是了,用数组记录一下,然后暴力找到一条链的端点(用度数判,暴力获得每个点的相对位置),再用线段树(?)维护下最值(找区间蔓延的最远地方)。
后来开空间时有些晕了,好像会MLE的样子,不管了到时间了,20分(应该)能拿到吧....
预计得分:60分
实际得分:40分
cena上链的情况栈溢出了,luogu上是MLE了,可怜我198行代码了qwq。不过暴力打成这样就海星了。

1 #include<cstdio> 2 #include<algorithm> 3 #include<queue> 4 #include<cstring> 5 #include<cmath> 6 #define maxnn 100090 7 8 using namespace std; 9 typedef long long ll; 10 11 int n,tot,lim,root; 12 ll ans; 13 int head[500],pre[500]; 14 int f[500][20],d[maxnn],lca[500][500]; 15 int du[maxnn]; 16 bool vis[maxnn]; 17 struct node{ 18 int to,next; 19 }edge[maxnn*2];// 改一下范围 迁就一下链的情况 20 struct SegmentTree{ 21 int l,r; 22 int maxn,minn; 23 }t[maxnn*4]; 24 25 void add(int x,int y) 26 { 27 edge[++tot].to=y; 28 edge[tot].next=head[x]; 29 head[x]=tot; 30 } 31 32 void dfs(int u,int fa) 33 { 34 for(int i=head[u];i;i=edge[i].next) 35 { 36 int v=edge[i].to; 37 if(v==fa) continue; 38 pre[v]=i; 39 dfs(v,u); 40 } 41 } 42 43 void init() 44 { 45 queue<int>q; 46 q.push(1),d[1]=1; 47 while(!q.empty()) 48 { 49 int u=q.front();q.pop(); 50 for(int i=head[u];i;i=edge[i].next) 51 { 52 int v=edge[i].to; 53 if(d[v]) continue; 54 d[v]=d[u]+1; 55 f[v][0]=u; 56 for(int j=1;j<=lim;j++) 57 f[v][j]=f[f[v][j-1]][j-1]; 58 q.push(v); 59 } 60 } 61 } 62 63 int Lca(int x,int y) 64 { 65 if(d[x]>d[y]) swap(x,y); 66 for(int i=lim;i>=0;i--) 67 if(d[f[y][i]]>=d[x]) y=f[y][i]; 68 if(x==y) return x; 69 for(int i=lim;i>=0;i--) 70 if(f[y][0]!=f[x][0]) y=f[y][0],x=f[x][0]; 71 return f[x][0]; 72 } 73 74 void pre_lca() 75 { 76 for(int i=1;i<=n;i++) 77 for(int j=i+1;j<=n;j++) 78 { 79 if(j==i+1) lca[i][j]=Lca(i,j); 80 else lca[i][j]=Lca(lca[i][j-1],j); 81 } 82 } 83 84 void work(int l,int r) 85 { 86 int fa=lca[l][r]; 87 ll tmp=0; 88 memset(vis,0,sizeof(vis)); 89 for(int i=l;i<=r;i++) 90 { 91 int orz=i; 92 while(orz!=fa) 93 { 94 if(!vis[pre[orz]]) tmp++,vis[pre[orz]]=1; 95 orz=f[orz][0]; 96 } 97 } 98 ans+=tmp; 99 } 100 101 void dfs_lace(int u) 102 { 103 vis[u]=1; 104 for(int i=head[u];i;i=edge[i].next) 105 { 106 int v=edge[i].to; 107 if(vis[v]) continue; 108 d[v]=d[u]+1; 109 dfs_lace(v); 110 } 111 } 112 113 void build(int p,int l,int r) 114 { 115 t[p].l=l,t[p].r=r; 116 if(l==r) 117 { 118 t[p].maxn=d[l]; 119 t[p].minn=d[l]; 120 return ; 121 } 122 int mid=(l+r)>>1; 123 build(p*2,l,mid); 124 build(p*2+1,mid+1,r); 125 t[p].maxn=max(t[p*2].maxn,t[p*2+1].maxn); 126 t[p].minn=min(t[p*2].minn,t[p*2+1].minn); 127 } 128 129 int ask1(int p,int l,int r) 130 { 131 if(t[p].l==l&&t[p].r==r) return t[p].maxn; 132 int mid=(t[p].l+t[p].r)>>1; 133 if(l>mid) return ask1(p*2+1,l,r); 134 else if(r<=mid) return ask1(p*2,l,r); 135 else return max(ask1(p*2,l,mid),ask1(p*2+1,mid+1,r)); 136 } 137 138 int ask2(int p,int l,int r) 139 { 140 if(t[p].l==l&&t[p].r==r) return t[p].minn; 141 int mid=(t[p].l+t[p].r)>>1; 142 if(l>mid) return ask2(p*2+1,l,r); 143 else if(r<=mid) return ask2(p*2,l,r); 144 else return min(ask2(p*2,l,mid),ask2(p*2+1,mid+1,r)); 145 } 146 147 int main() 148 { 149 freopen("treecnt.in","r",stdin); 150 freopen("treecnt.out","w",stdout); 151 scanf("%d",&n); 152 if(n>3000) 153 { 154 for(int i=1;i<=n-1;i++) 155 { 156 int x=0,y=0; 157 scanf("%d%d",&x,&y); 158 add(x,y),add(y,x); 159 du[x]++;du[y]++; 160 } 161 for(int i=1;i<=n;i++) 162 if(du[i]==1) 163 { 164 root=i; 165 break; 166 } 167 d[root]=1; 168 dfs_lace(root); 169 build(1,1,n); 170 for(int i=1;i<=n;i++) 171 for(int j=i+1;j<=n;j++) 172 { 173 int qwq=ask1(1,i,j); 174 int orz=ask2(1,i,j); 175 ans+=qwq-orz; 176 } 177 printf("%lld",ans); 178 return 0; 179 } 180 lim=log2(n)+1; 181 for(int i=1;i<=n-1;i++) 182 { 183 int x=0,y=0; 184 scanf("%d%d",&x,&y); 185 add(x,y),add(y,x); 186 } 187 dfs(1,0); 188 for(int i=1;i<=n;i++) 189 pre[i]=(pre[i]+1)>>1; 190 init(); 191 pre_lca(); 192 // 开始乱搞n^3logn 193 for(int i=1;i<=n;i++) 194 for(int j=i+1;j<=n;j++) 195 work(i,j); 196 printf("%lld ",ans); 197 return 0; 198 }
正解:鸽了qwq。
今天补上
期望得分:100+60+60=220
实际得分:100+30+40=170
暴力分打的比以前多了,但还是比期望少了很多,出现了很多意料外的问题...
小结:今天的题目感觉比较简单的样子,感觉暴力分好打而且分多==没想到是Day2的难度,T1就考树不资瓷,然后三道题都可能用的倍增 ,这样真的好么qwq。没有我最不擅长的dp就很资瓷,因为我连普及组的dp水平都达不到。而且出了两道树上的问题,我还是比较擅长的,很资瓷。否则我绝对拿不到人生中第一个也是最后一个rank1(大概是因为有Dalao挂题了以及今天获得了生日buff)然后吐槽一下题解,就会说暴力枚举判断,不能说详细一些嘛(逃)。
另:不会明天考dp吧qwq。
