题目大意:给定平面上n个点,找出其中的一对点的距离,使得在这n个点的所有点对中,该距离为所有点对中最小的。$n$<=100000。
$Algorithm$
最朴素的$n^2$枚举肯定是不行了,我们在这个数量级只能考虑$nlogn$做法。那么与这个数量级比较相关的也就是分治了。 把整个平面分为两个部分,分别求出两个部分点对间最小的距离,之后再处理跨区域的情况。
• 分治法求解步骤: O(NlogN) by hzwer
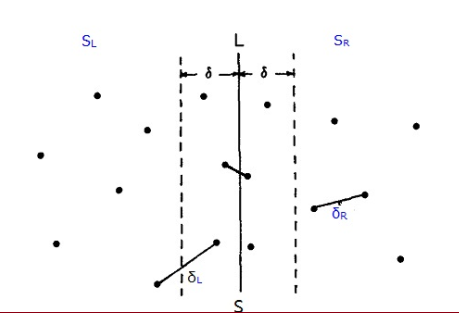
1 将点集 S 分为两个⼦集 SL 和 SR 分别求解
2 记 δ 为⼦集中求得的最优值(min(δL; δR)),合并两个集合求
解。
图中以分界线为中⼼,任何⼀个 2δ · 2δ 的正⽅形内,只有常
数个点,暴⼒ for 过去就好了。
$Code$

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 5 using namespace std; 6 7 int n; 8 int que[200090]; 9 struct node{ 10 double x,y; 11 }p[200090]; 12 bool cmp(node a,node b) 13 { 14 return a.x<b.x; 15 } 16 17 bool cmp2(int a,int b) 18 { 19 return p[a].y<p[b].y; 20 } 21 22 double dis(int i,int j) 23 { 24 return sqrt((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y)); 25 } 26 27 double merge(int l,int r) 28 { 29 double dd=1e8; 30 if(l==r) return dd; 31 if(l+1==r) return dis(l,r); 32 int mid=(l+r)>>1; 33 double dl=merge(l,mid); 34 double dr=merge(mid+1,r); 35 dd=min(dl,dr); 36 37 int pos=0; 38 for(int i=l;i<=r;i++) 39 if(fabs(p[mid].x-p[i].x)<dd) que[++pos]=i; 40 sort(que+1,que+1+pos,cmp2); 41 for(int i=1;i<=pos;i++) 42 for(int j=i+1;j<=pos;j++) 43 { 44 if(dis(que[i],que[j])>dd) break; 45 double ddd=dis(que[i],que[j]); 46 dd=min(dd,ddd); 47 } 48 return dd; 49 } 50 51 int main() 52 { 53 scanf("%d",&n); 54 for(int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y); 55 sort(p+1,p+1+n,cmp); 56 printf("%.4lf",merge(1,n)); 57 return 0; 58 }
几个注意事项
- 边界的处理。
if(l==r) return dd; if(l+1==r) return dis(l,r);
- 利用正方形里有常数个点的性质时,要及时$break$。否则会超时。
- 图中的$L$线大概是$mid$。开始找点的时候距离与他比较。
