[数据结构] 如何判断一个链表是否有环? 环的入口? 环的长度?

练习算法的时候, 遇到这个问题, 感觉挺有意思的, 所以记录下来.

在网上参考了这个答案:
https://blog.csdn.net/thefutureisour/article/details/8174313

但是后来又自己想了一下, 用自己的思维思考了一遍, 感觉更加清晰明了.

问题是:

1. 如何判断一个链表是否有环?
2. 环的长度如何计算?
3. 如何找到环的入口?

我们先看图说话:

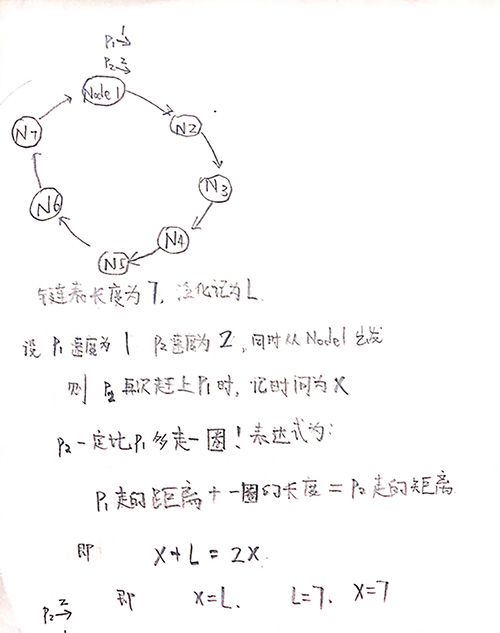
假设链表长度为7, 我们用 L 表示, 设有两个指针, P1和P2, 速度分别为1, 2, (P1 一次走1个结点, P1 一次走2个结点), 同时从 Node1出发.
那么请问: 何时P2再次赶上P1呢? 这是一个很有意思的问题. 就像以前的运动会长跑跑圈一样, 快的总会追上慢的.

我们要明白一个道理:
无论 P1 转了几圈, P2 第一次追上 P1 的时候, P2 一定比 P1 多走一圈而已!!

我们设 时间为 X 时, P2追上P1, 有表达式:
P1走的距离 + 一圈的长度 = P2走的距离
即为:
X * 1 + L = X * 2
化简为:
X = L
L = 7, 所以, P1和P2从 Node1出发后又一次且是第一次在 Node1相遇, 因为刚好走了一圈, 一圈长度为7.

我们再来看一个复杂的情况:
假设链表不是整个环, 而是从中间某一点开始有环的. 那么好像一下复杂了不少, 一下子有点绕不过弯了呢! 我是这样子的, 所以我想了好一会.
我们先来看图.

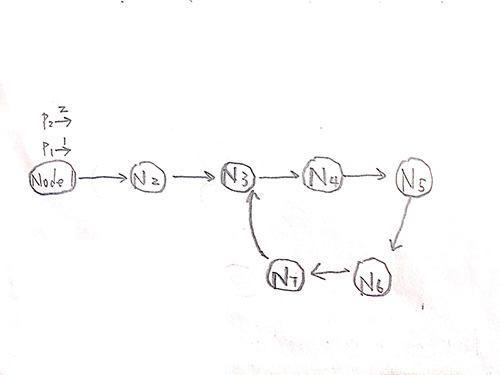
但是道理还是一样的.
无论环的入口在哪里,
无论 P1 和P2 在环里转了几圈, P2 第一次追上 P1 的时候, P2 一定比 P1 多走一圈环的长度而已!!

我们设 时间为 X 时, P2追上P1, 有表达式:
P1走的距离 + 此时环一圈的长度(记为C) = P2走的距离
即为:
X * 1 + C = X * 2
化简为:
X = C

在这张图中, 我们知道 C=5, P1和P2在 Node6处相遇, 因为是从 Node1出发的, P1走了5个时间单位, 速度为1.

更加一般的情况是, C = (V2-V1)* X, V2代表P2的速度, V1代表P1的速度, 我们为了方便表示, 简单令其为2 和 1 罢了.
既然我们知道了C的长度, 那么如何求 环的入口呢?

有两种办法:

1. 用链表的长度 L 减去C, 即可得到从出发点走几步,就到了 环的入口. 比如这里, 7-5=2, 走两步, 环的入口是Node3.
2. 如果我们没有求出C的长度怎么玩呢?
   我们知道, 环的入口, 其实也是链表的尾结点, 和Node1的距离, 是L-C, 因为环的长度为C, 链表总长度为L, 而这段不在环内.

同时, 我们记相遇点为 NodeX, NodeX到 环的入口, 也就是尾结点的距离, 为 L-C. ? 如何理解, 下面是证明步骤:

因为P1从Node1出发走了X个时间长度单位到NodeX, 而剩下的长度为L-X, 而C=X.
所以, 所以NodeX到环的入口的距离为 L-C,
如果此时 再让 另一个指针P3 以和P1相同的速度出发往前走, 那么, P1和P3必然在环的入口相遇.